From
Tabular Q-Learning
to
DQN
GitHub Repository
Outline
- RL 101 refresher
- Tabular Q-Learning
- RL as a regression problem (Fitted Q Iteration)
- From FQI to Deep Q-Network (DQN)
Motivation
Stable-Baselines3 (SB3)
from stable_baselines3 import DQN # SAC, TD3, TQC are all successors of DQN from stable_baselines3 import SAC, TD3 from sb3_contrib import TQC # Instantiate the algorithm on the Lunar Lander env model = DQN("MlpPolicy", "LunarLander-v2", verbose=1) # Train for 100 000 steps model.learn(100_000, progress_bar=True)
from stable_baselines3 import DQN # SAC, TD3, TQC are all successors of DQN from stable_baselines3 import SAC, TD3 from sb3_contrib import TQC # Instantiate the algorithm on the Lunar Lander env model = DQN("MlpPolicy", "LunarLander-v2", verbose=1) # Train for 100 000 steps model.learn(100_000, progress_bar=True)
RL from scratch
Raffin et al. "Learning to Exploit Elastic Actuators for Quadruped Locomotion.": https://github.com/araffin/sbx
Flappy Bird
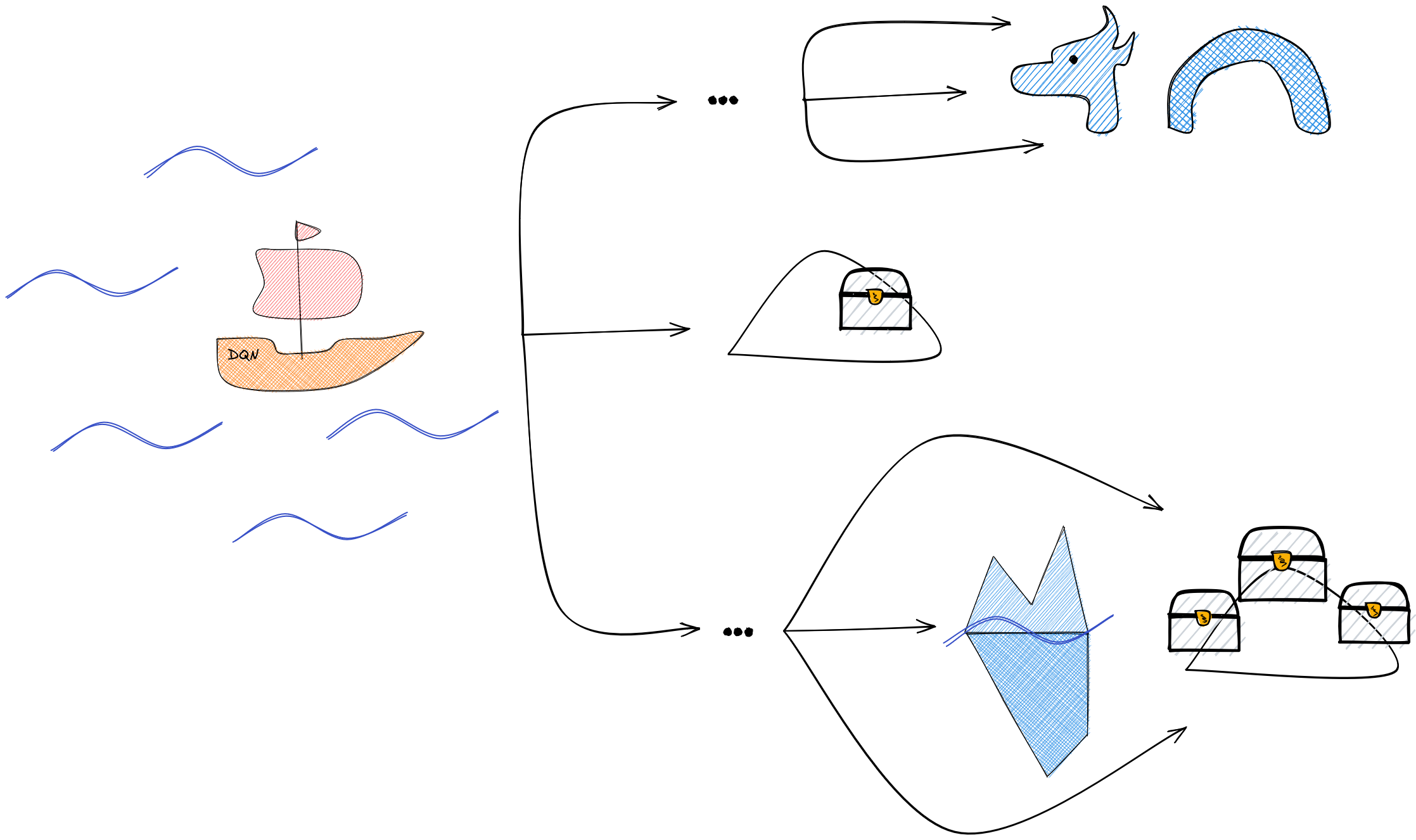
RL 101 (1/2)
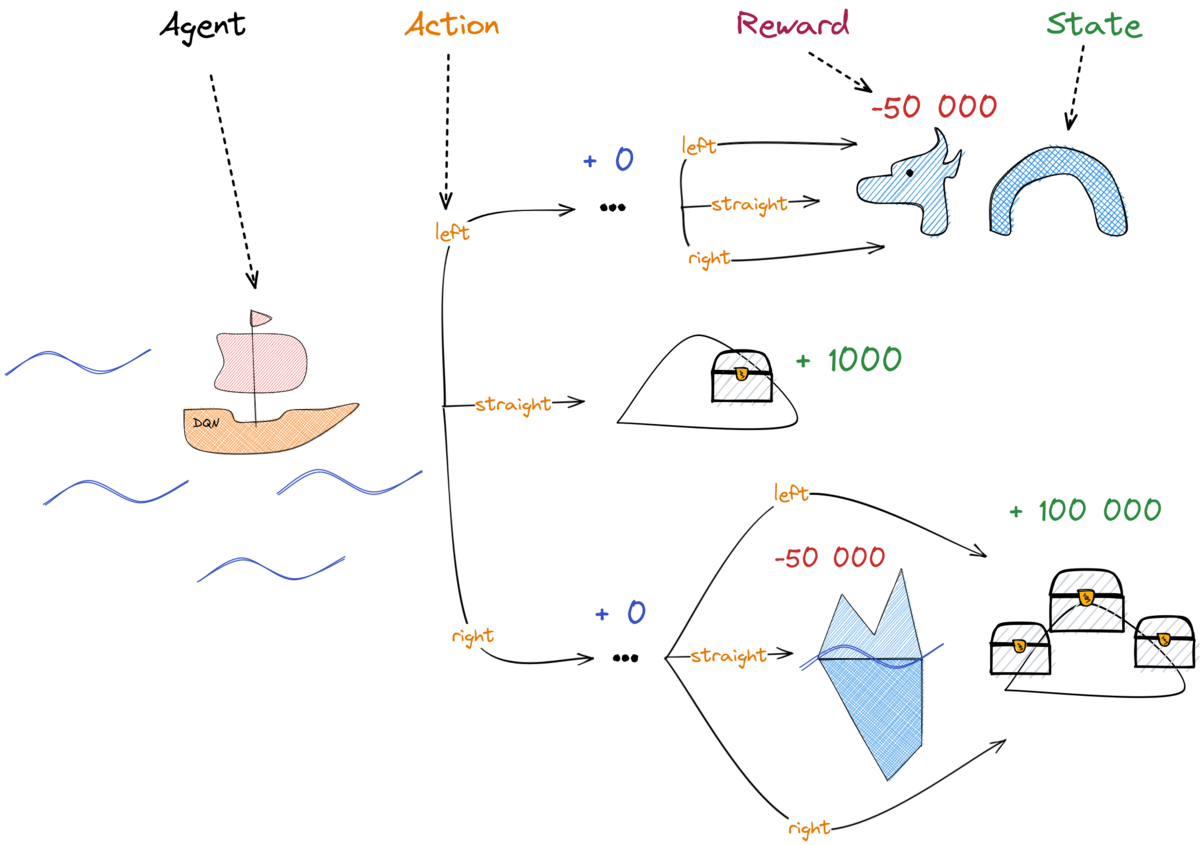
RL 101 (2/2)
- Agent: the "boat", our main character
- State: Where are we? (position, speed, ...)
- Action: What can we do? (steer left, right, ...)
- Reward: How good are we doing?
- Policy: The "captain", defines the agent's behavior
Value Functions
How good is it to be in this state?
Win: 1.0 | Draw: 0.5 | Lose: 0.0
Depends on the state
Depends on the policy
Source: Freek Stulp - Master AIC
Action-Value Function: Q-Value
What if we have no model?
Solution: Qπ(s,a) instead of Vπ(s)
Qπ(s,a)=E[rt+γrt+1+γ2rt+2+...∣st=s,at=a].
π(s)=a∈AargmaxQπ(s,a)
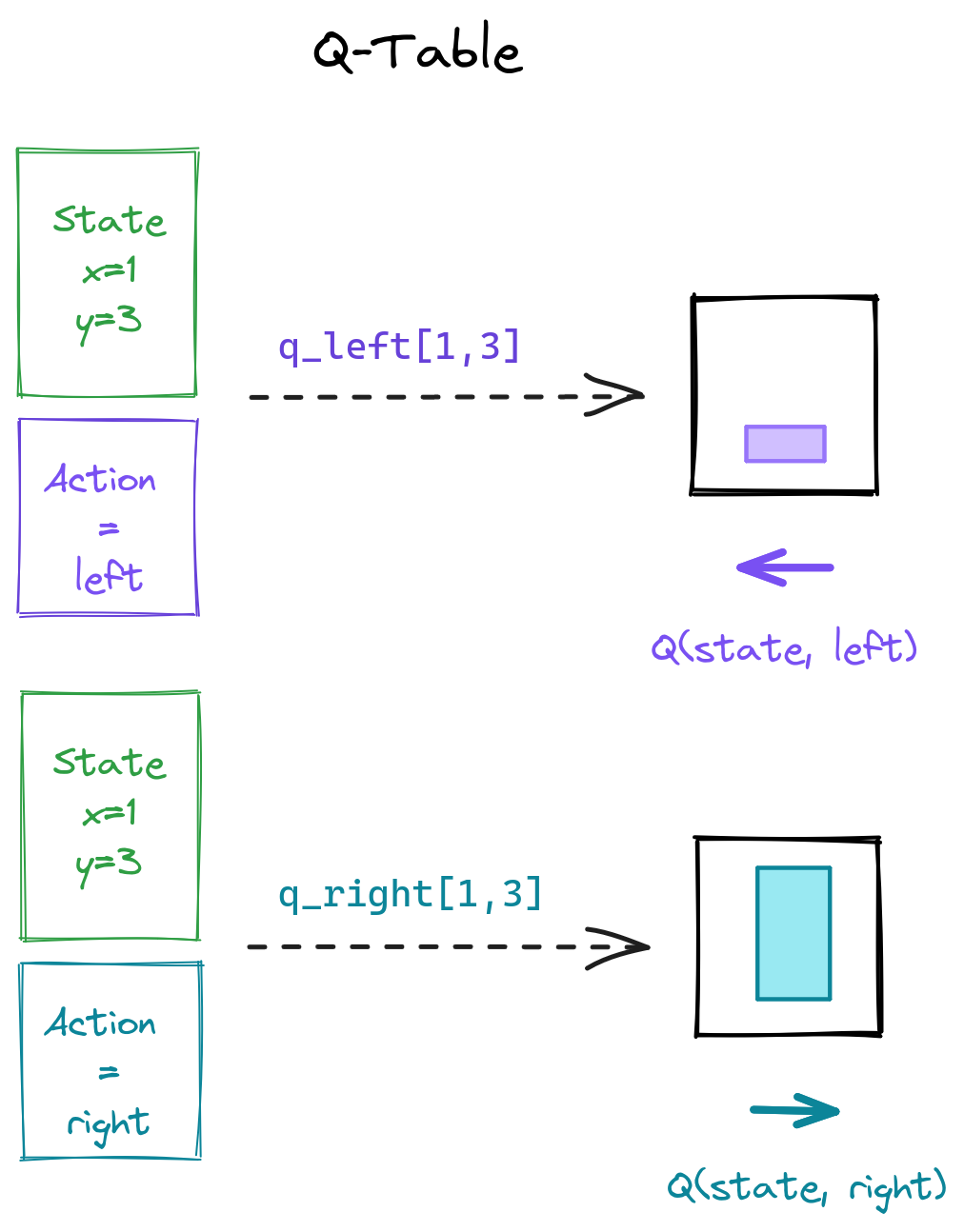
Tabular Q-Learning: Discrete States
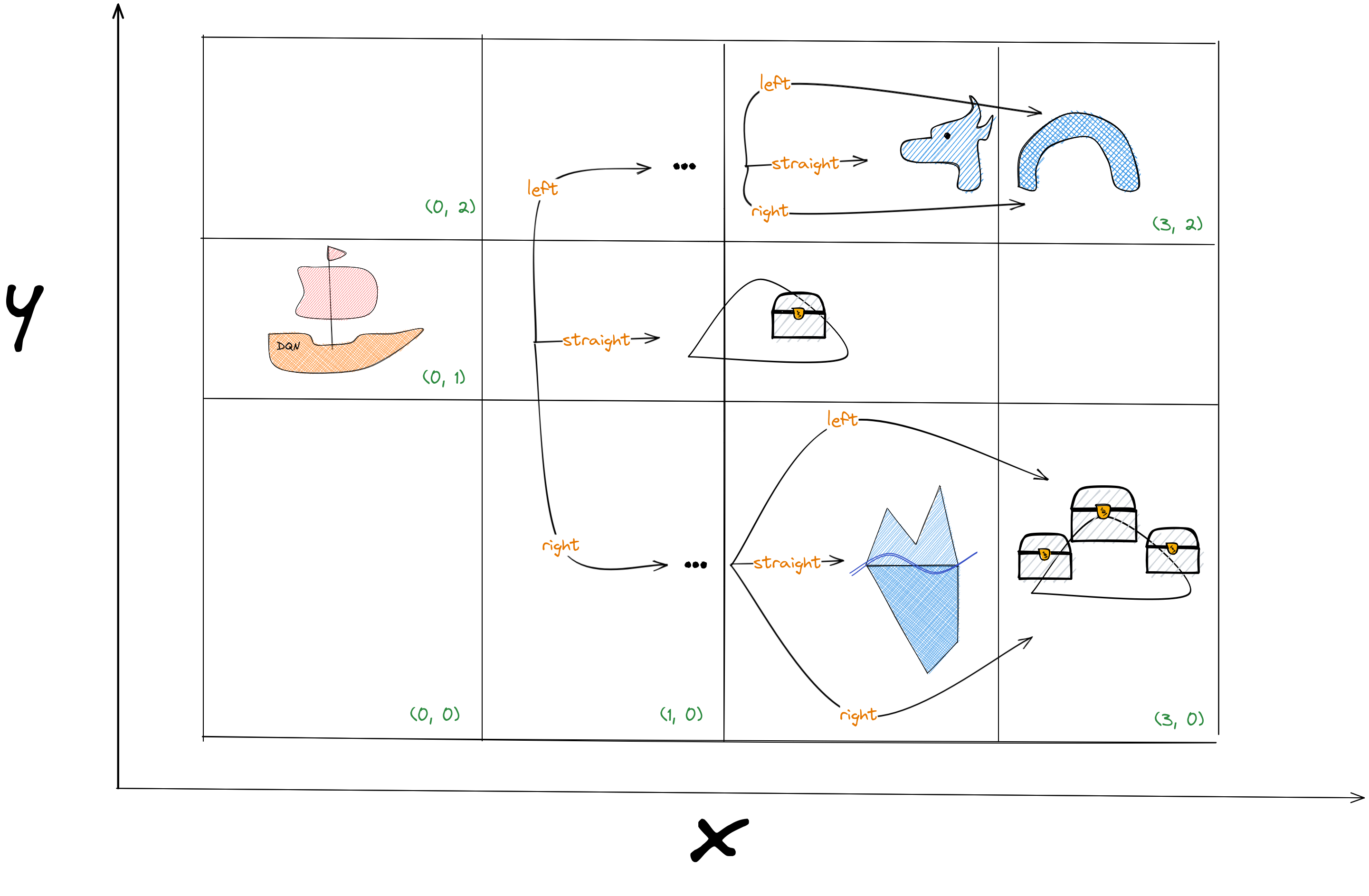
Tabular Q-Learning: Q-table
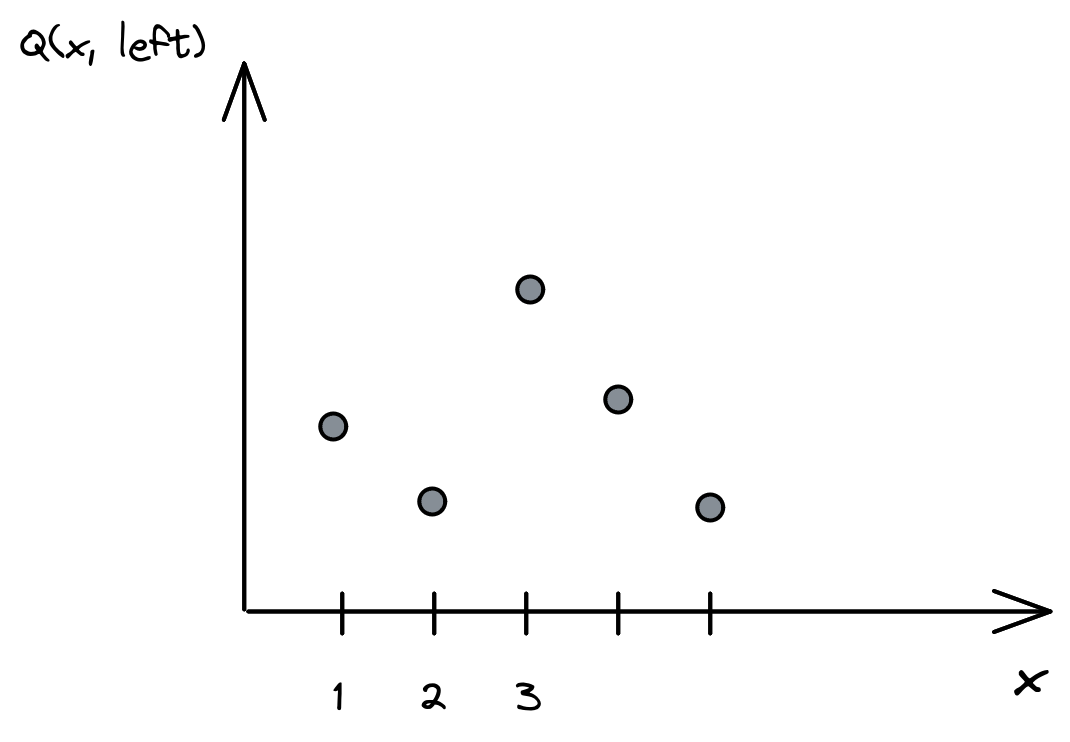
Tabular Q-Learning: Q-values
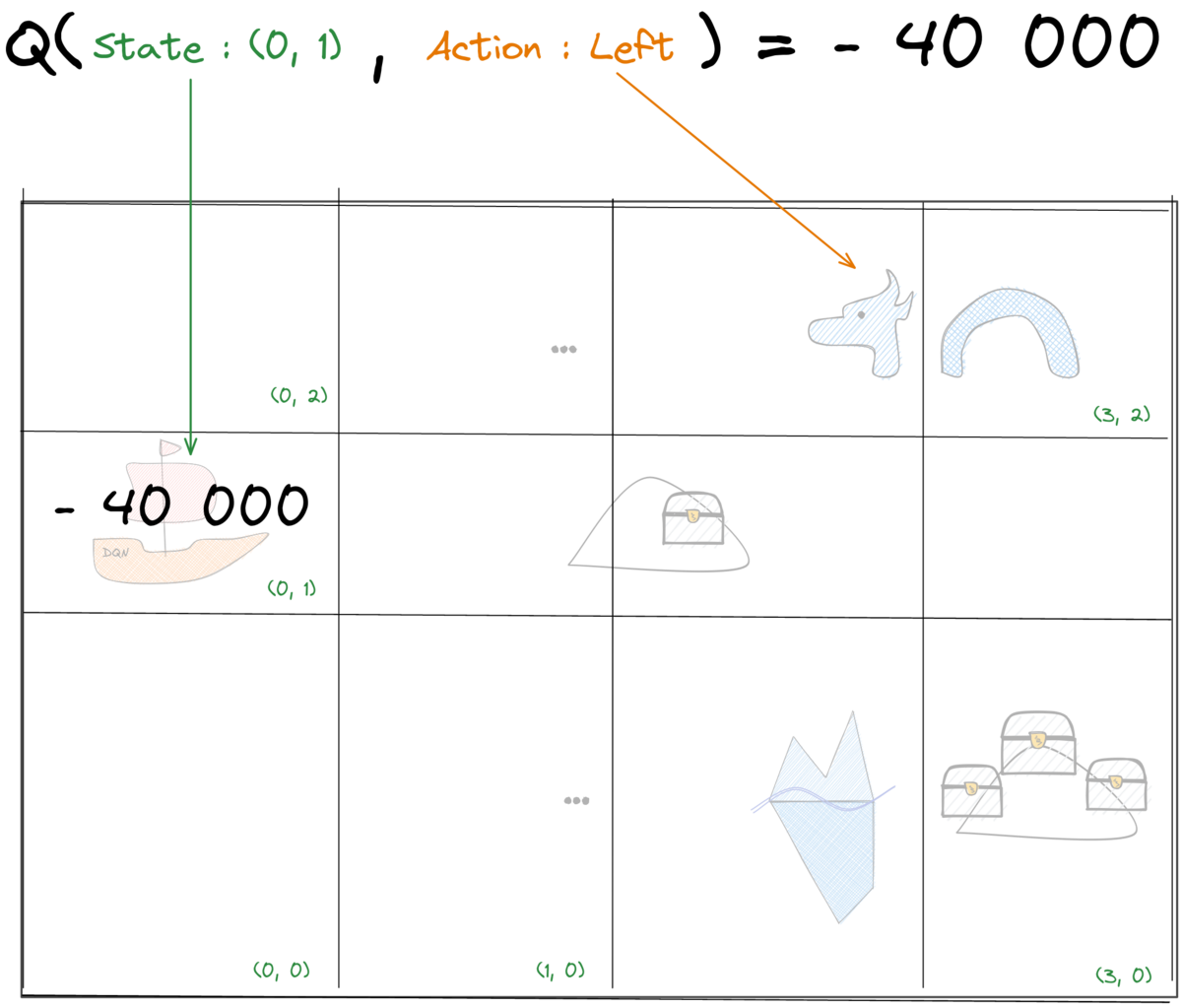
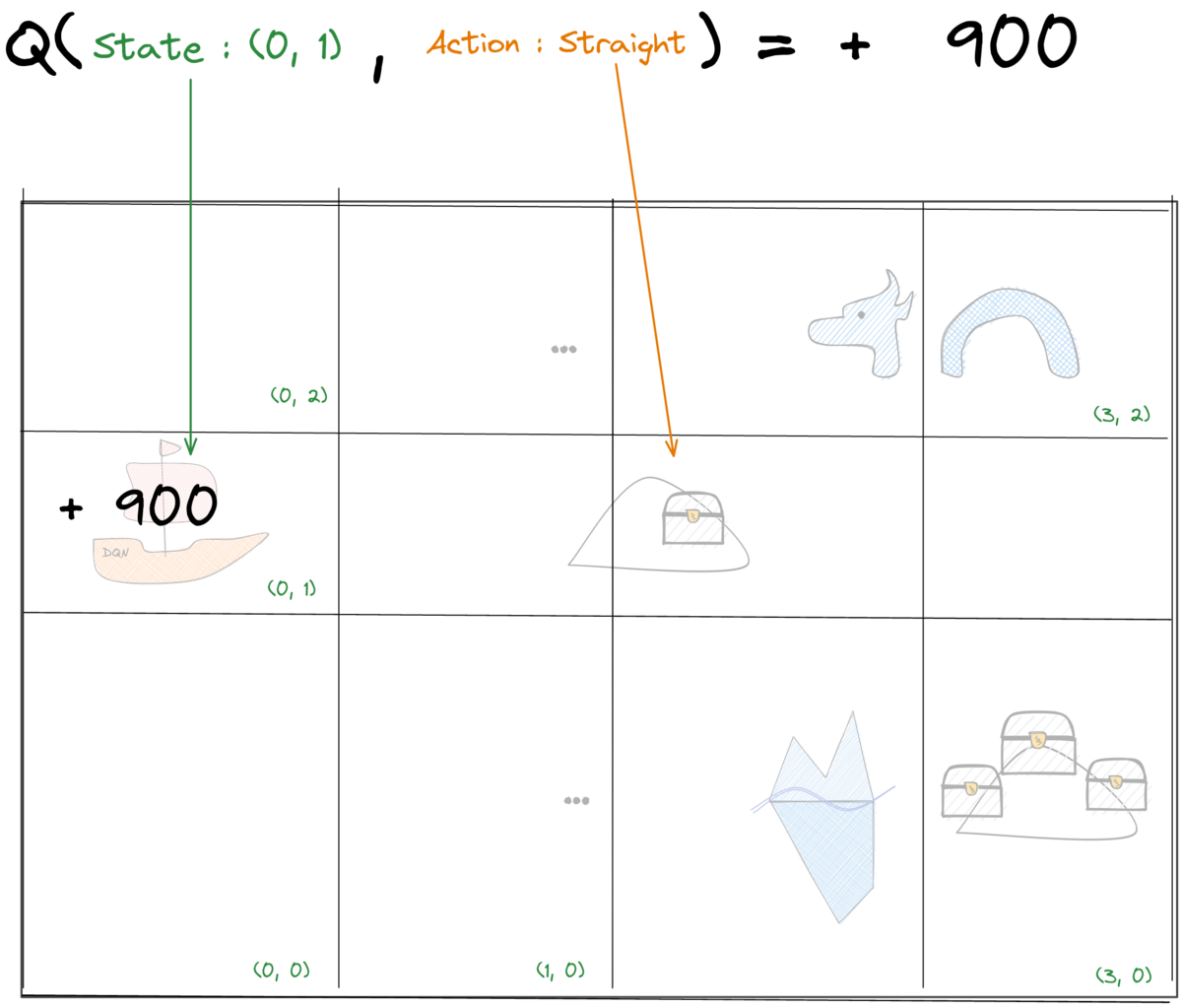
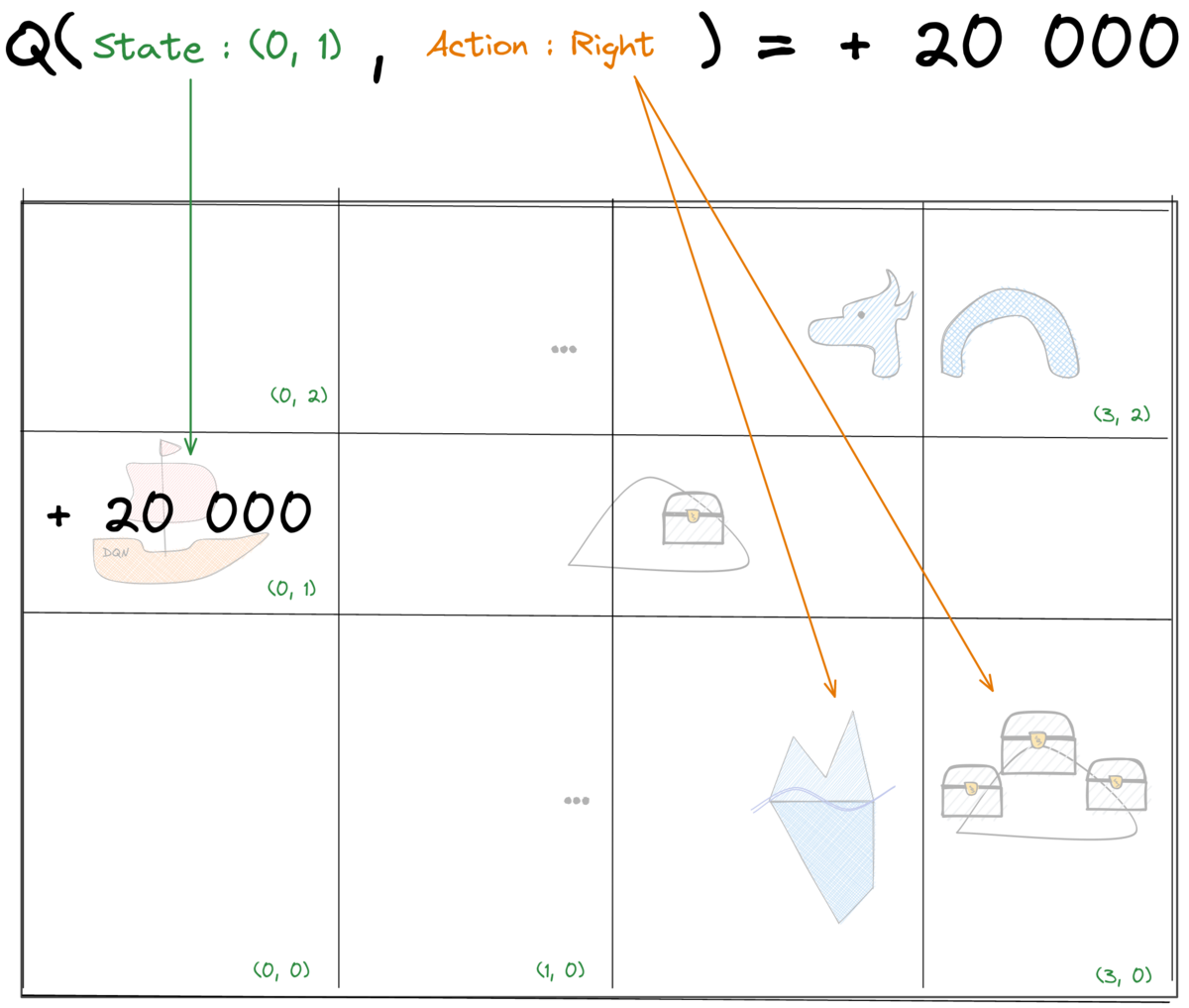
Tabular Q-Learning: Update rule
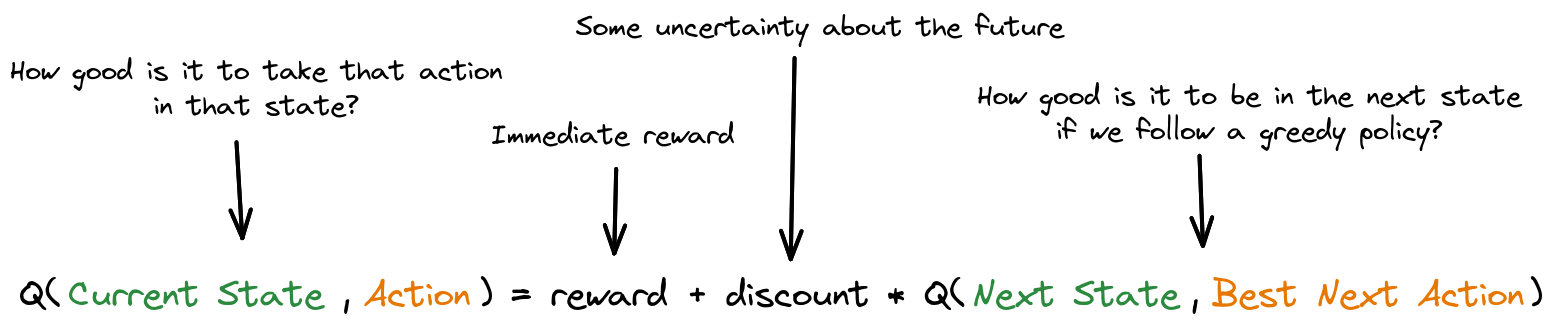
Bellman equation for optimal value function:
Q∗(st,at)=E[r(st,at)+γa′maxQ∗(st+1,a′)].
Q-learning update rule
Qn(st,at)←Qn−1(st,at)+α⋅(rt+γ⋅a′maxQn−1(st+1,a′)−Qn−1(st,at))
Tabular Q-Learning: Update explained
α=1 (learning rate)
Q(st,at)=rt+γ⋅a′maxQ(st+1,a′)
Reminder
Tabular Q-Learning: Terminal State
Questions?
Tabular Q-Learning: Limitations
- Discrete states
- No generalization (lookup table)
- Discrete actions
How to go beyond tabular Q-Learning?
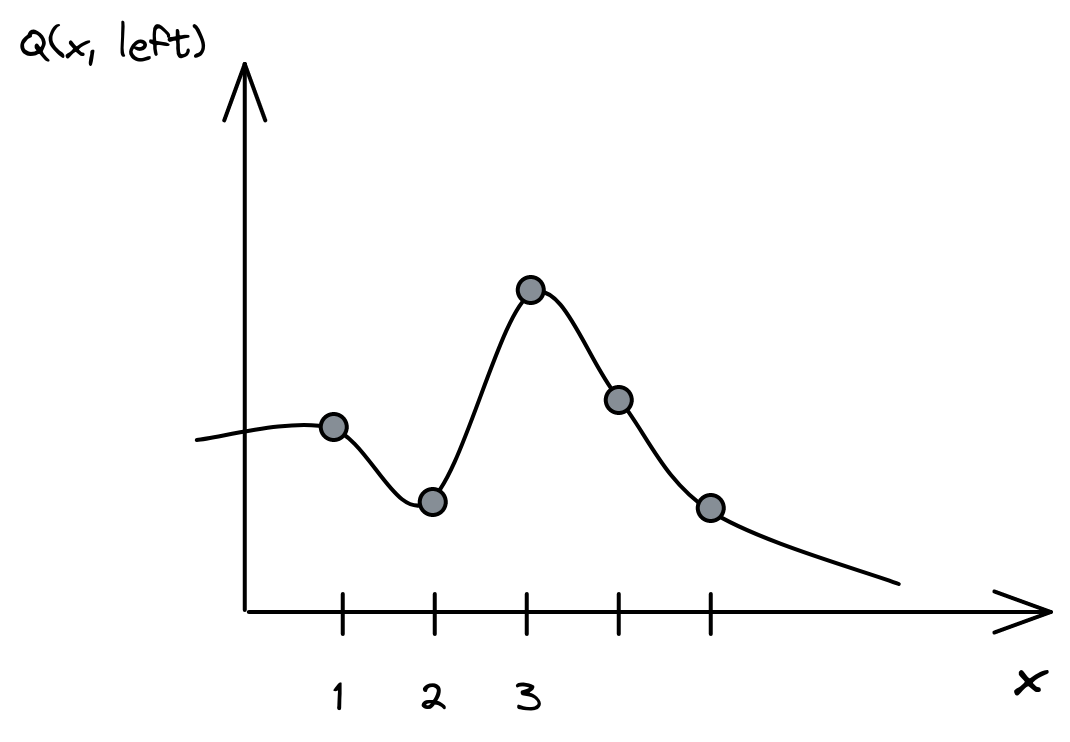
Q-Value Estimator
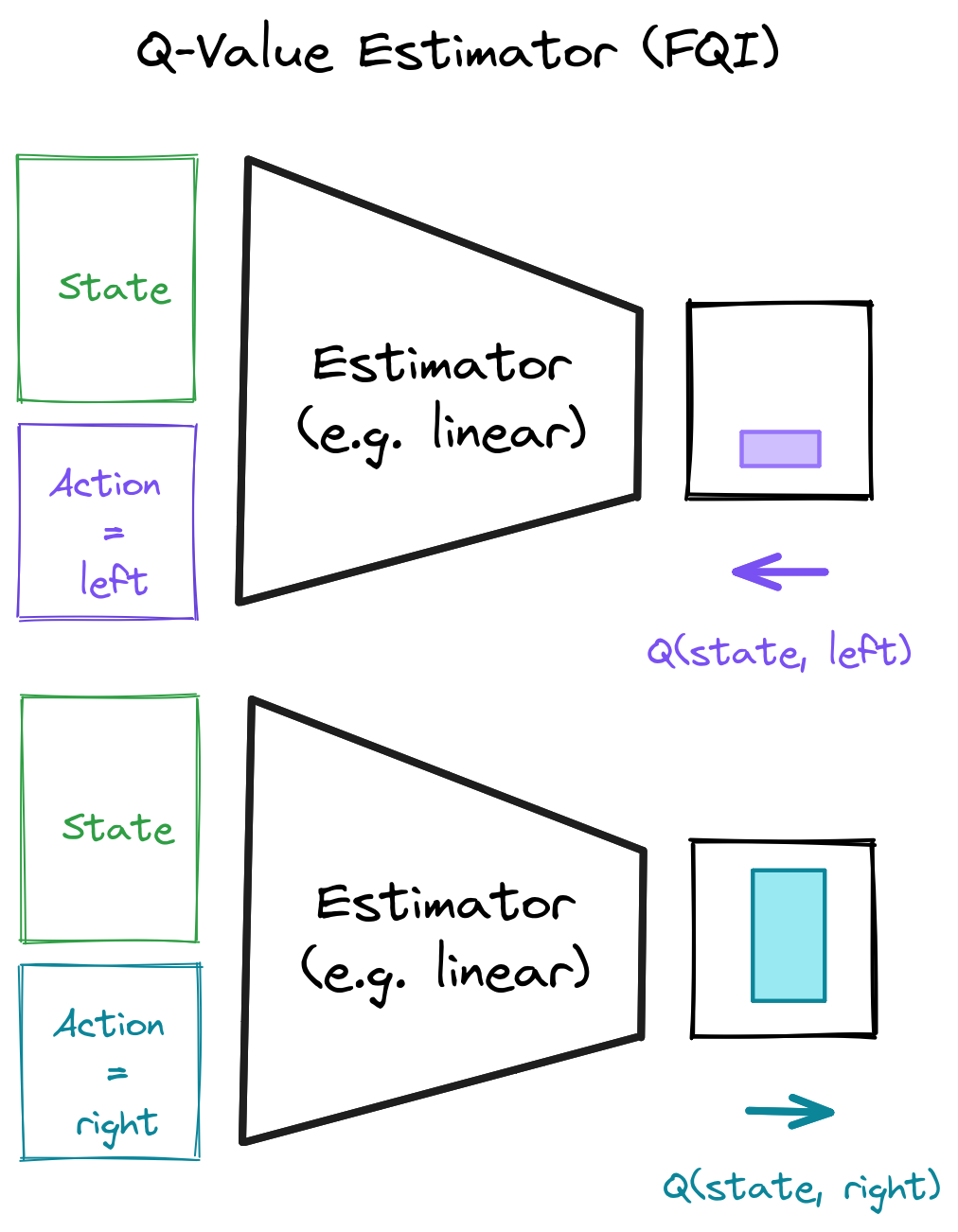
Q-Learning Regression (1/2)
Qθ(st,at)=rt+γ⋅a′∈Amax(Qθ(st+1,a′))
fθ(x)=y
θ: parameters of the estimator
One small detail...
Qθ(st,at) depends on Qθ(st+1,a′)...
What can we do about it?
Iterate! Use Qθn(st,at)
Fitted Q-Iteration (FQI) (1/2)
- Create the training set based on the previous iteration Qθn−1(s,a) and the transitions:
- input: x=(st,at)
- if st+1 is non terminal: y=rt+γ⋅maxa′∈A(Qθn−1(st+1,a′))
- if st+1 is terminal: y=rt
- Fit a model using a regression algorithm to obtain Qθn(s,a)
fθ(x)=y
- Repeat, n=n+1
Fitted Q-Iteration (2/2)
For n=0, the initial training set is defined as:
- x=(st,at)
- y=rt
Fitted Q-Iteration (code)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
initial_targets = rewards # Initial Q-value estimate qf_input = np.concatenate((states, actions)) qf_model.fit(qf_input, initial_targets) for _ in range(N_ITERATIONS): # Re-use Q-value model from previous iteration # to create the next targets next_q_values = get_max_q_values(qf_model, next_states) # Non-terminal states target targets[non_terminal_states] = rewards + gamma * next_q_values # Special case for terminal states targets[terminal_states] = rewards # Update Q-value estimate qf_model.fit(qf_input, targets)
CartPole Env
https://gymnasium.farama.org/environments/classic_control/cart_pole/
Gym/Gymnasium API
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
import gymnasium as gym # Create the environment env = gym.make("CartPole-v1", render_mode="human") # Reset env and get first observation obs, _ = env.reset() # Step in the env with random actions and display the env for _ in range(100): env.render() # Display the env action = env.action_space.sample() # Retrieve new observation, reward, # termination signal, truncation signal # and additional infos next_obs, reward, terminated, truncated, info = env.step(action) # Update current observation obs = next_obs # End of an episode if terminated or truncated: obs, _ = env.reset()
FQI in practice (1st notebook)
FQI Limitations
- Offline RL
- Loop over all possible actions A to get next best action a′: a′∈AmaxQθ(st+1,a′)
- Instability (target depends on Qθn−1(st+1,a′))
From FQI to DQN
- Offline RL → Online RL
- Loop over actions → One forward pass to get all Qθ(s,a)
- Instability → Target Network Qθ′(s,a)
Questions?
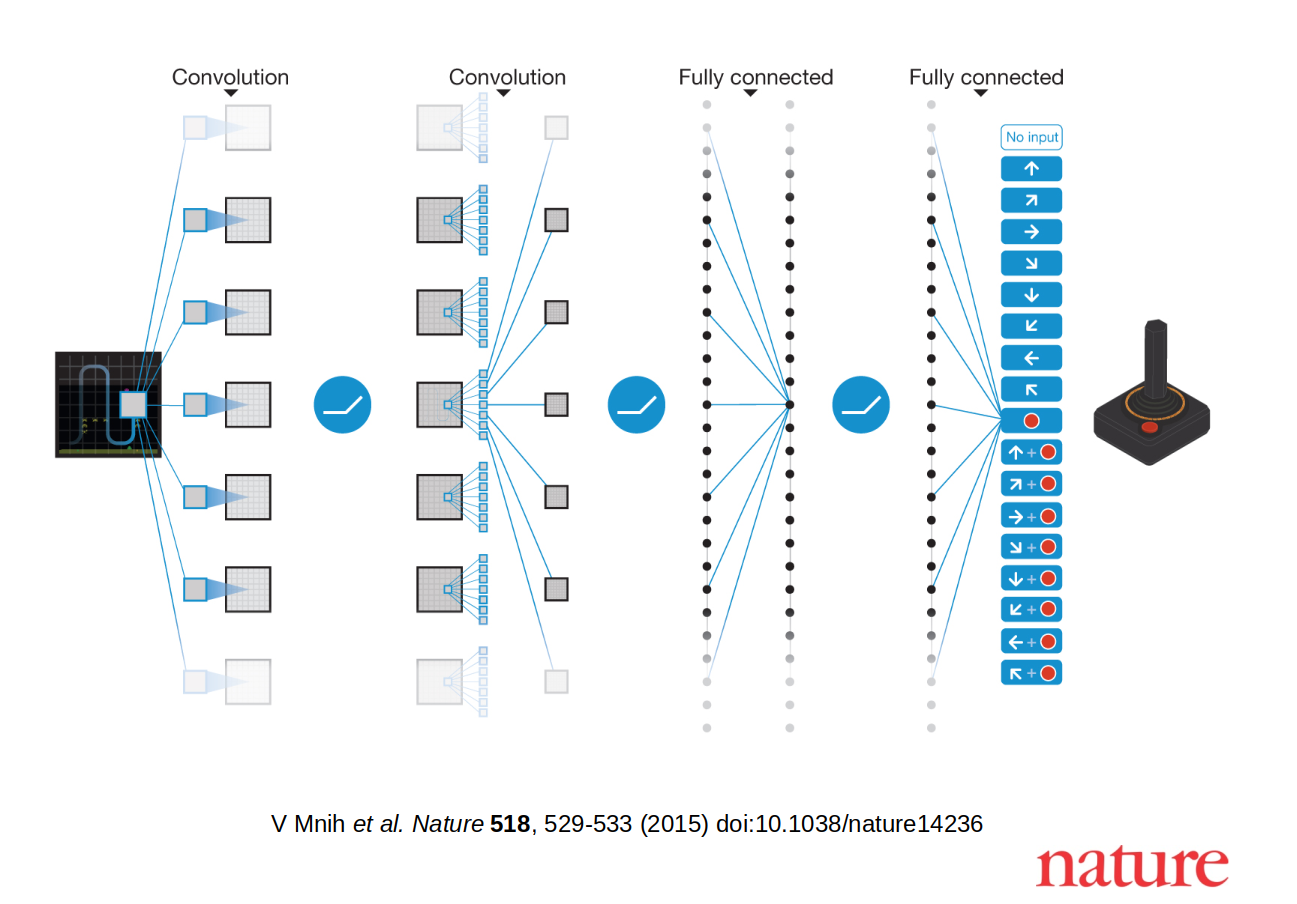
Deep Q-Network (DQN)
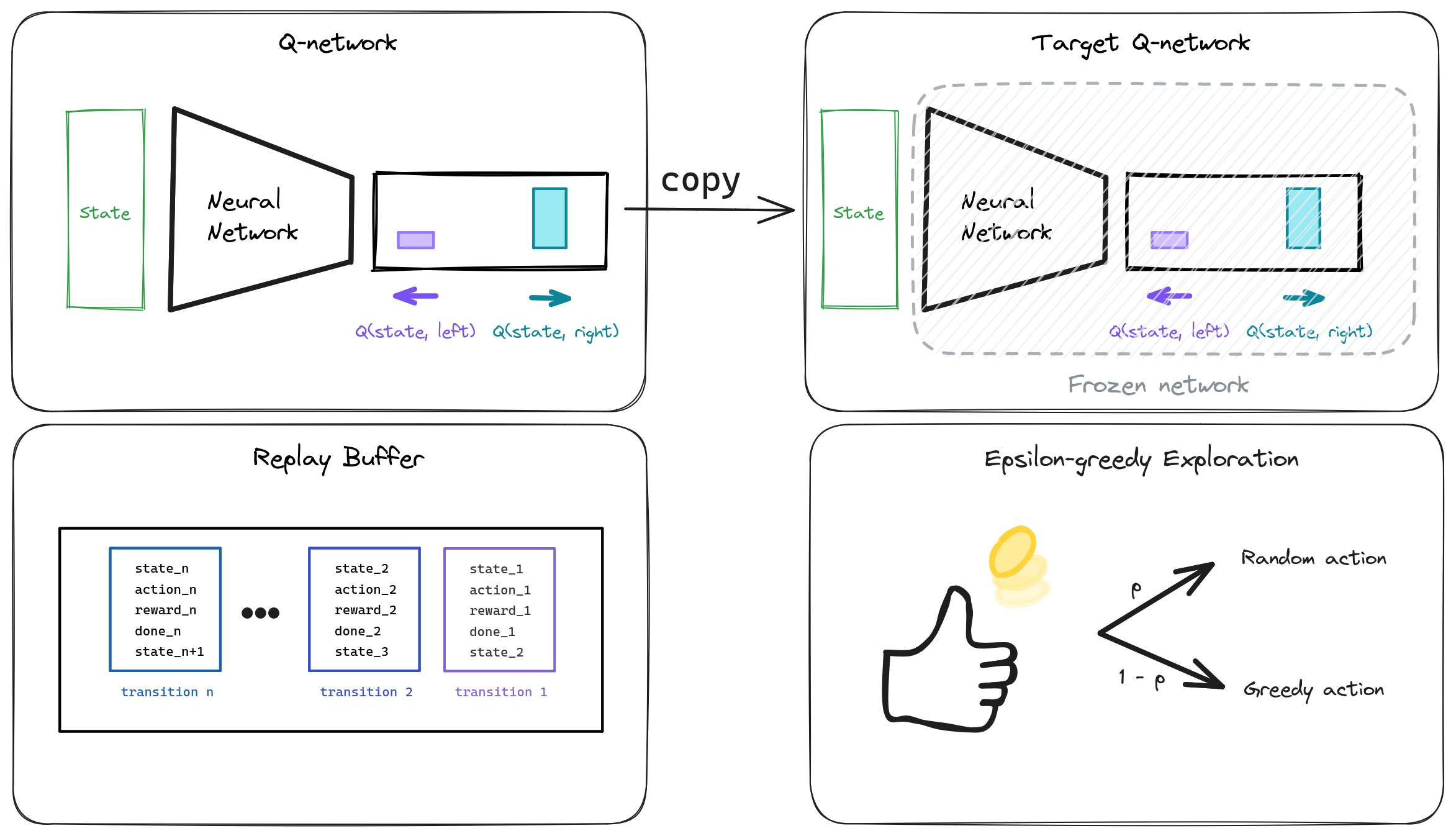
Replay Buffer
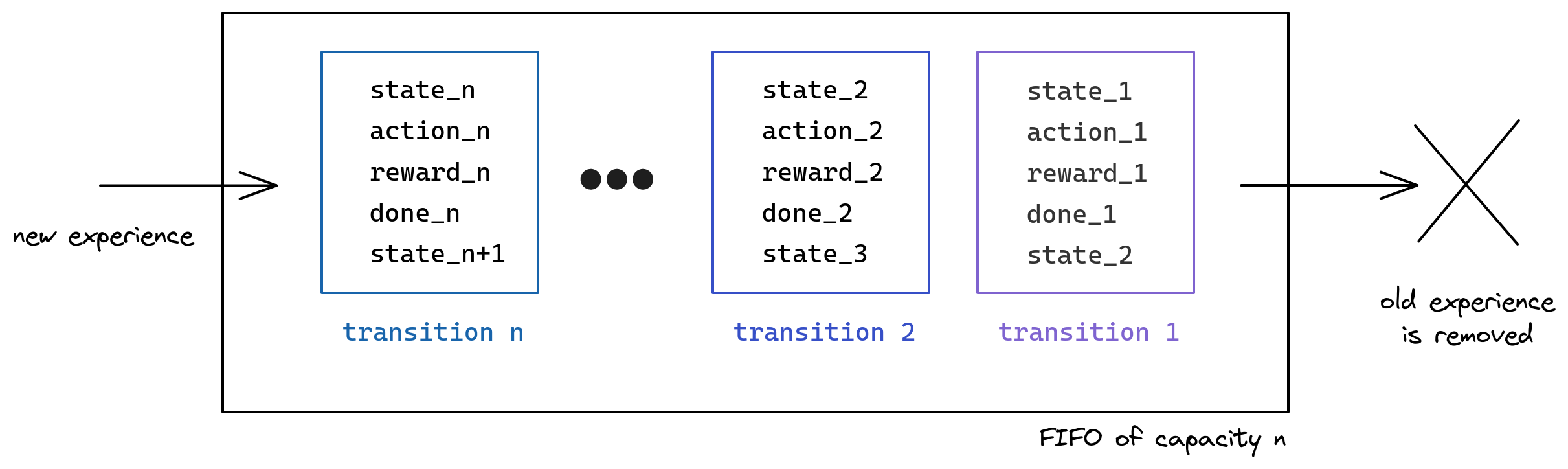
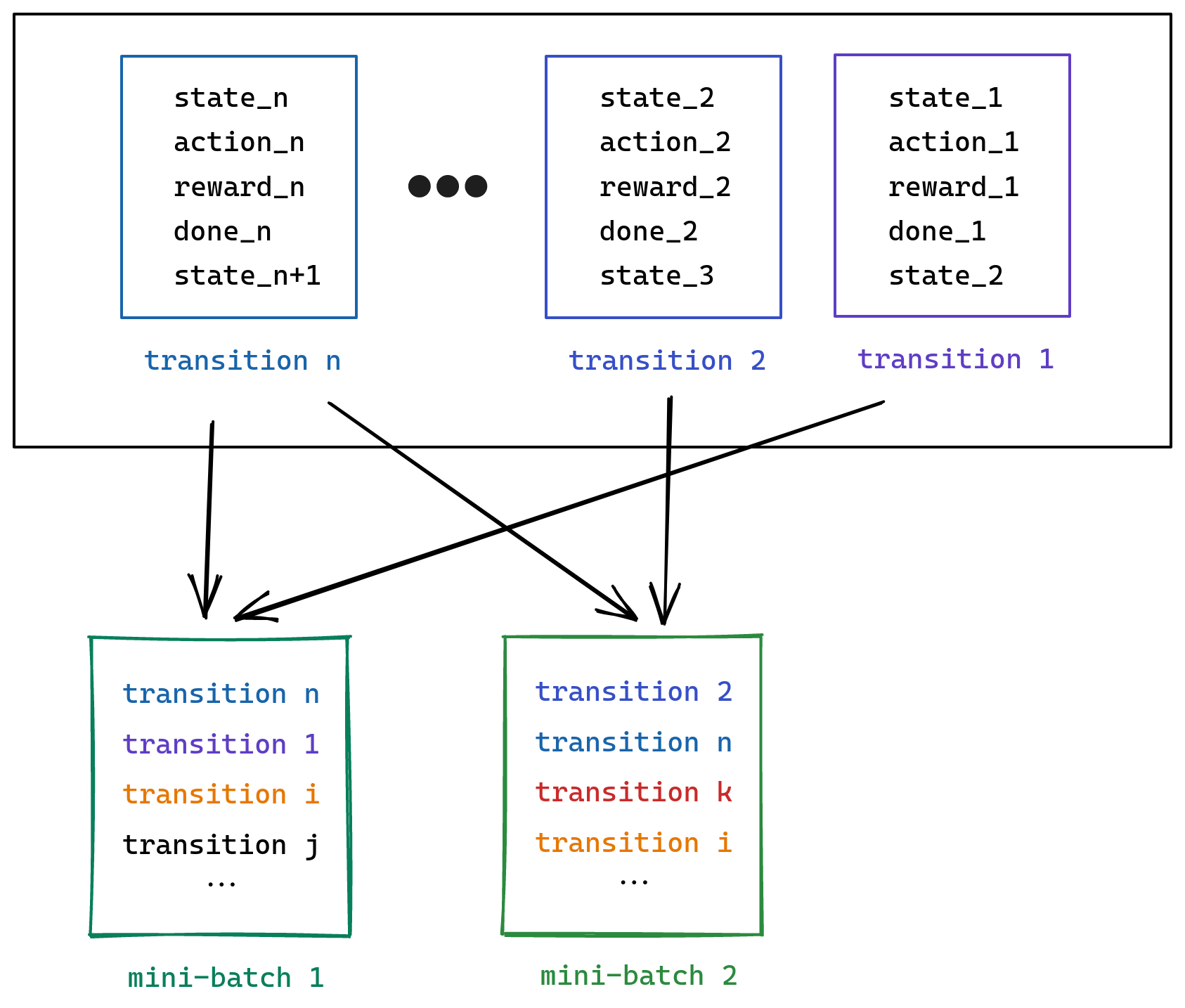
Replay Buffer Sampling
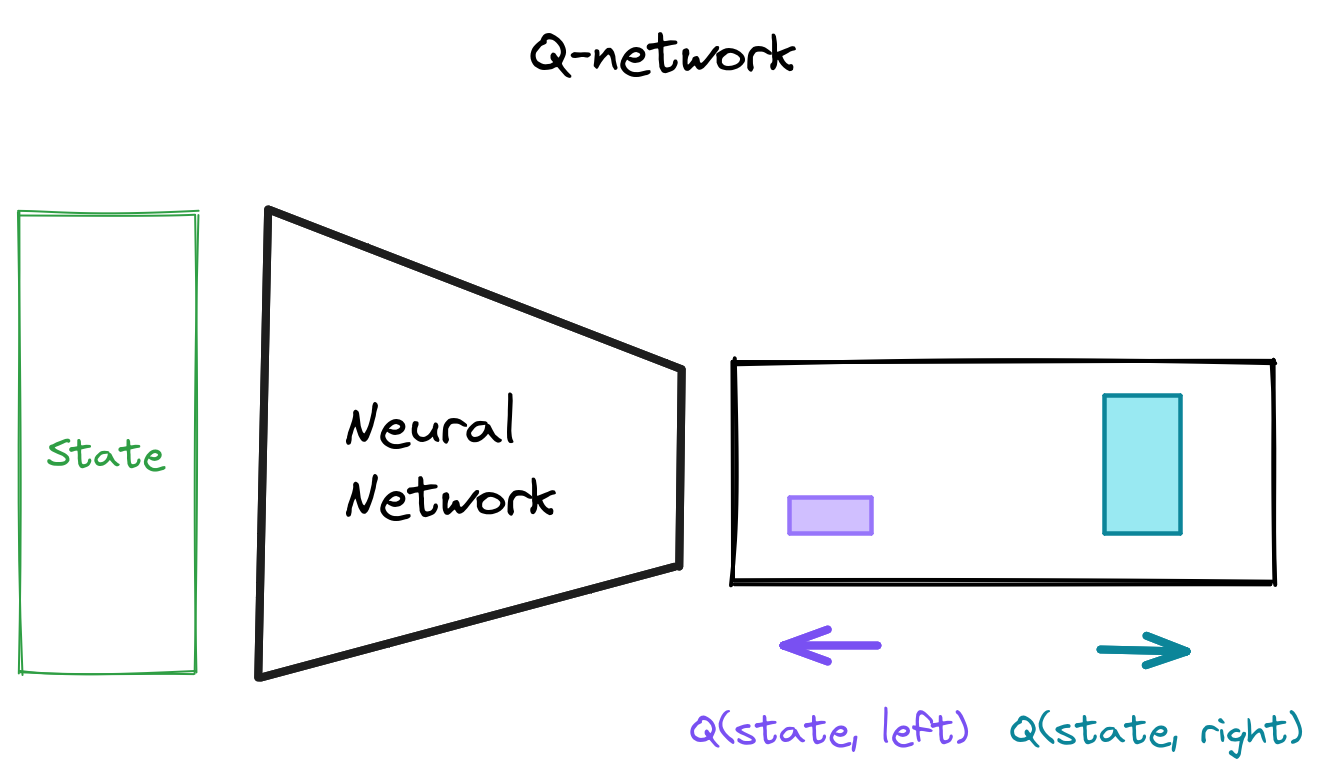
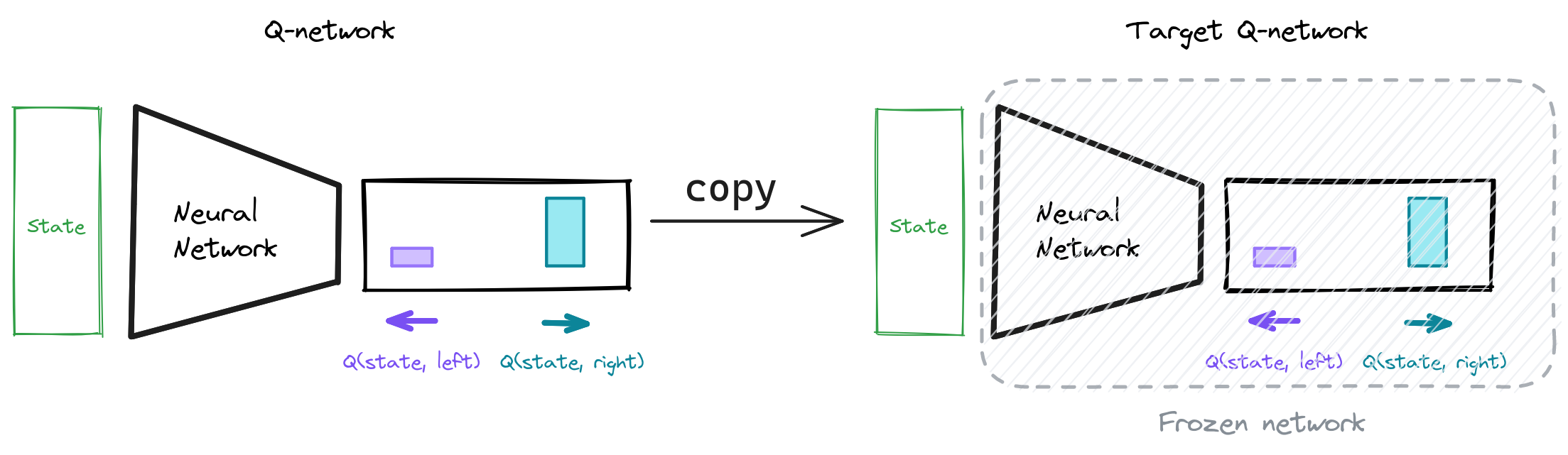
Q-network
The training loop
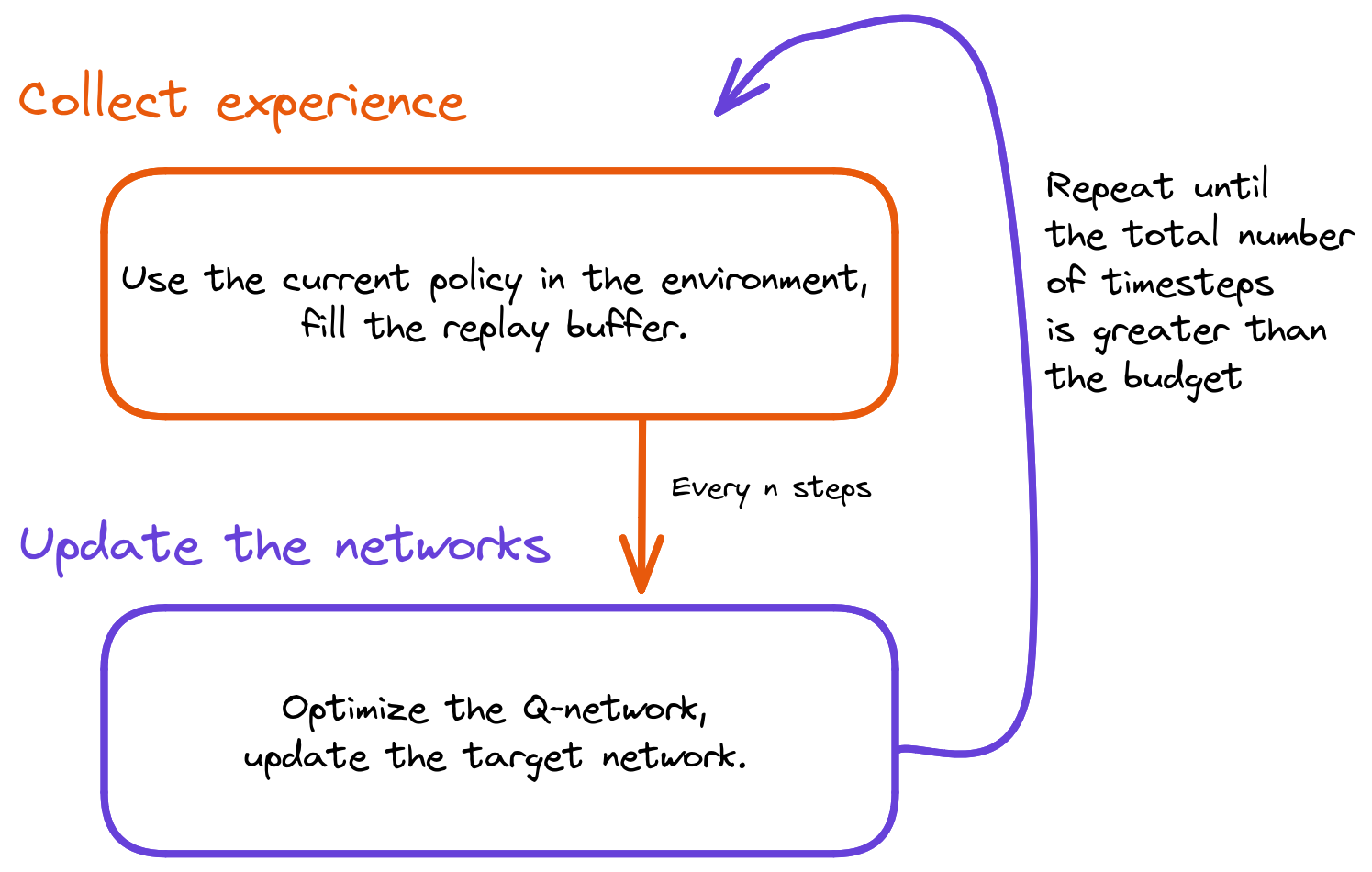
Collecting Experience
# Retrieve q values for the current observation q_values = q_model(current_obs) # Follow greedy-policy: # take the action with the highest q_value action = np.argmax(q_values) # Do one step in the env next_obs, reward, terminated, _, _ = env.step(action) # Store transition in the replay buffer replay_buffer.store(obs, action, reward, terminated, next_obs)
# Retrieve q values for the current observation q_values = q_model(current_obs) # Follow greedy-policy: # take the action with the highest q_value action = np.argmax(q_values) # Do one step in the env next_obs, reward, terminated, _, _ = env.step(action) # Store transition in the replay buffer replay_buffer.store(obs, action, reward, terminated, next_obs)
# Retrieve q values for the current observation q_values = q_model(current_obs) # Follow greedy-policy: # take the action with the highest q_value action = np.argmax(q_values) # Do one step in the env next_obs, reward, terminated, _, _ = env.step(action) # Store transition in the replay buffer replay_buffer.store(obs, action, reward, terminated, next_obs)
# Retrieve q values for the current observation q_values = q_model(current_obs) # Follow greedy-policy: # take the action with the highest q_value action = np.argmax(q_values) # Do one step in the env next_obs, reward, terminated, _, _ = env.step(action) # Store transition in the replay buffer replay_buffer.store(obs, action, reward, terminated, next_obs)
# Retrieve q values for the current observation q_values = q_model(current_obs) # Follow greedy-policy: # take the action with the highest q_value action = np.argmax(q_values) # Do one step in the env next_obs, reward, terminated, _, _ = env.step(action) # Store transition in the replay buffer replay_buffer.store(obs, action, reward, terminated, next_obs)
Exploration / Exploitation
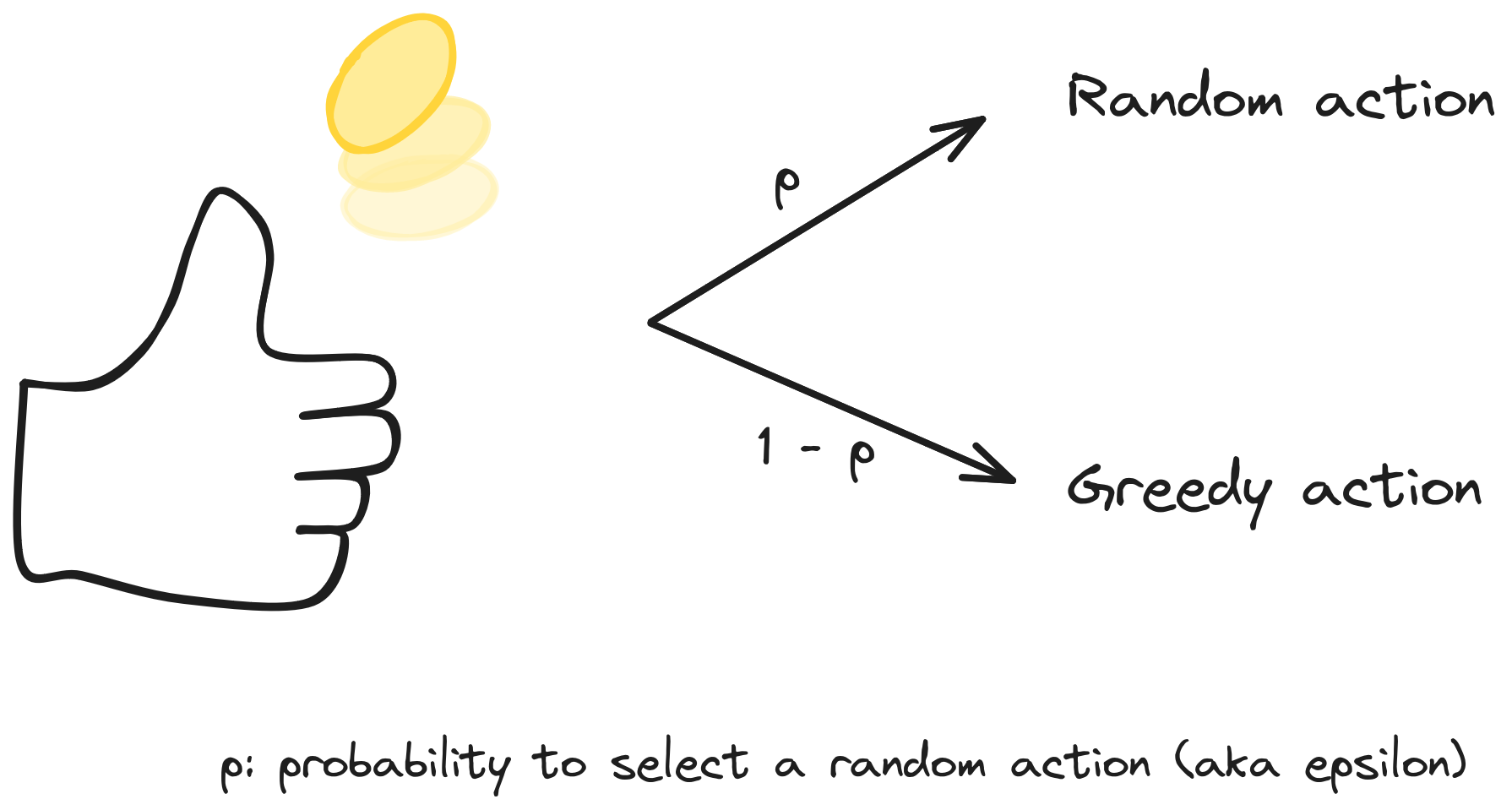
Epsilon-greedy Exploration
# Flip a biased coin take_random_action = np.random.rand() < exploration_rate if take_random_action: # Random action action = action_space.sample() else: # Greedy action action = np.argmax(q_values)
# Flip a biased coin take_random_action = np.random.rand() < exploration_rate if take_random_action: # Random action action = action_space.sample() else: # Greedy action action = np.argmax(q_values)
# Flip a biased coin take_random_action = np.random.rand() < exploration_rate if take_random_action: # Random action action = action_space.sample() else: # Greedy action action = np.argmax(q_values)
# Flip a biased coin take_random_action = np.random.rand() < exploration_rate if take_random_action: # Random action action = action_space.sample() else: # Greedy action action = np.argmax(q_values)
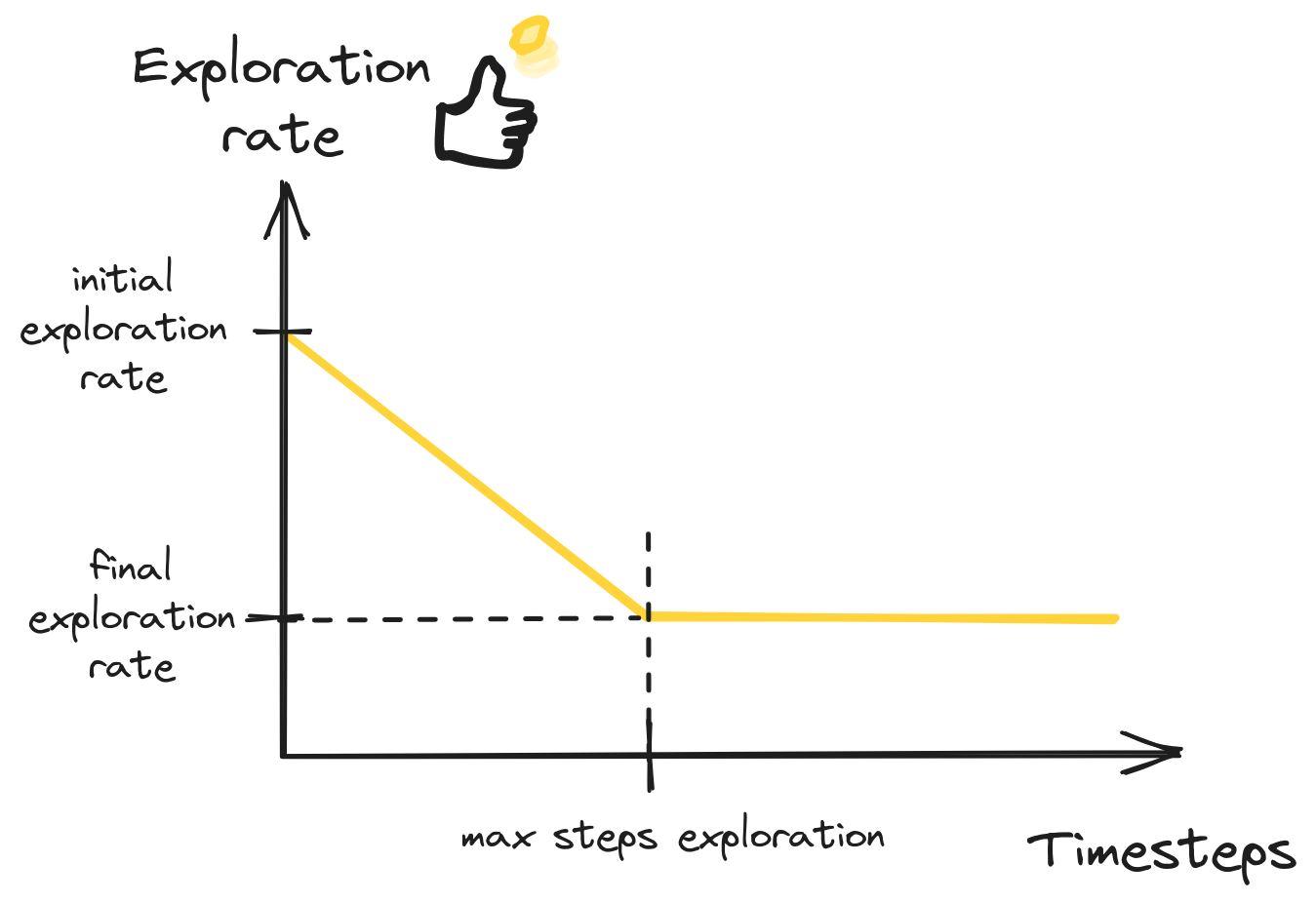
Exploration Schedule
Annotated DQN Algorithm
Target Q-Network
DQN Overview
Questions?
PyTorch API
| NumPy | PyTorch |
|---|---|
np.array([[1, 2], [3, 4]]) |
th.tensor([[1, 2], [3, 4]]) |
np.ones((2, 3)) |
th.ones(2, 3) |
np.concatenate |
th.cat |
x.shape |
x.shape |
x.argmax(axis=...) |
x.argmax(dim=...) |
x.item() |
x.item() |
| NumPy to PyTorch: | th.as_tensor |
Backup Slides
Regression 101
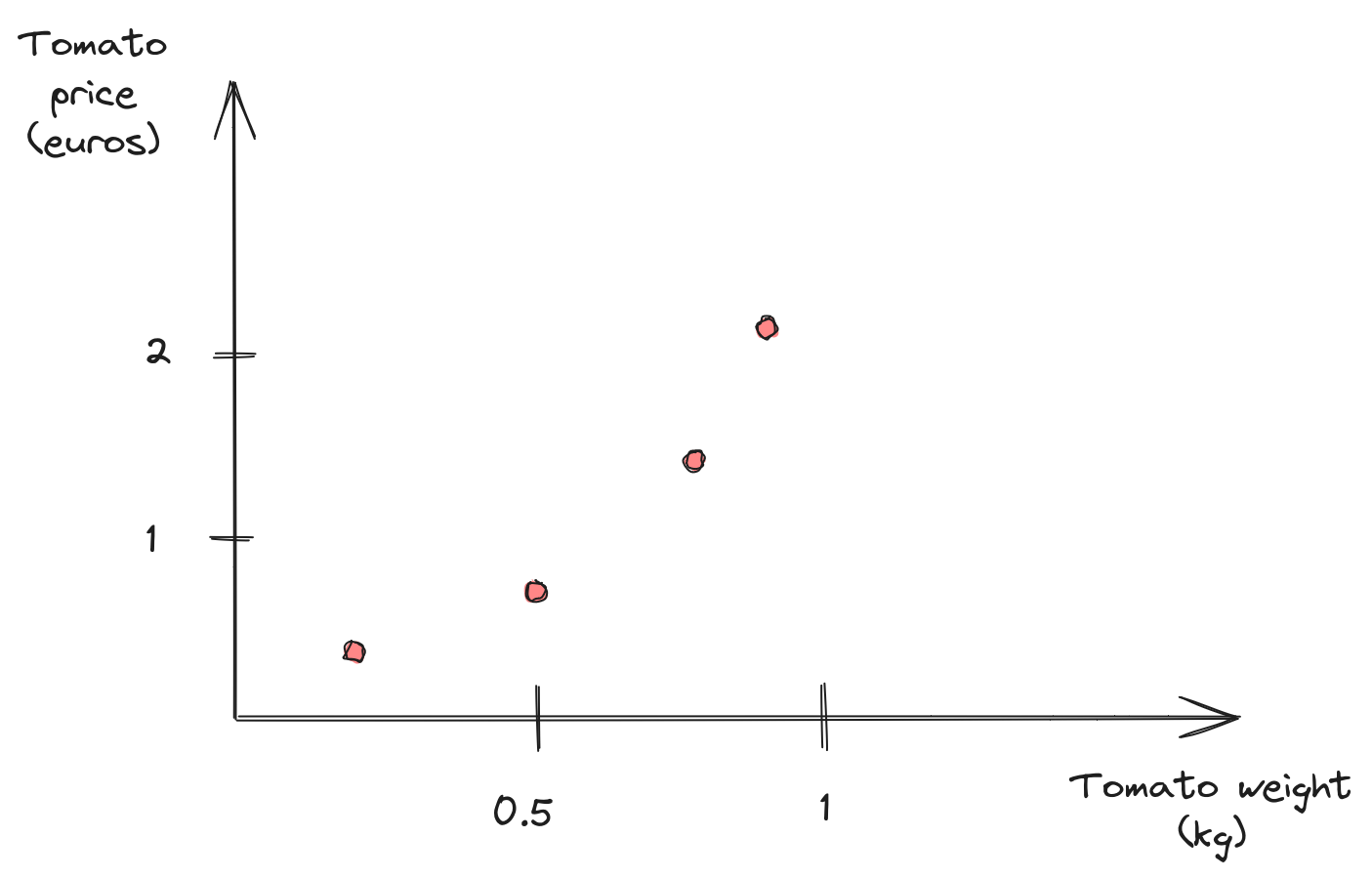
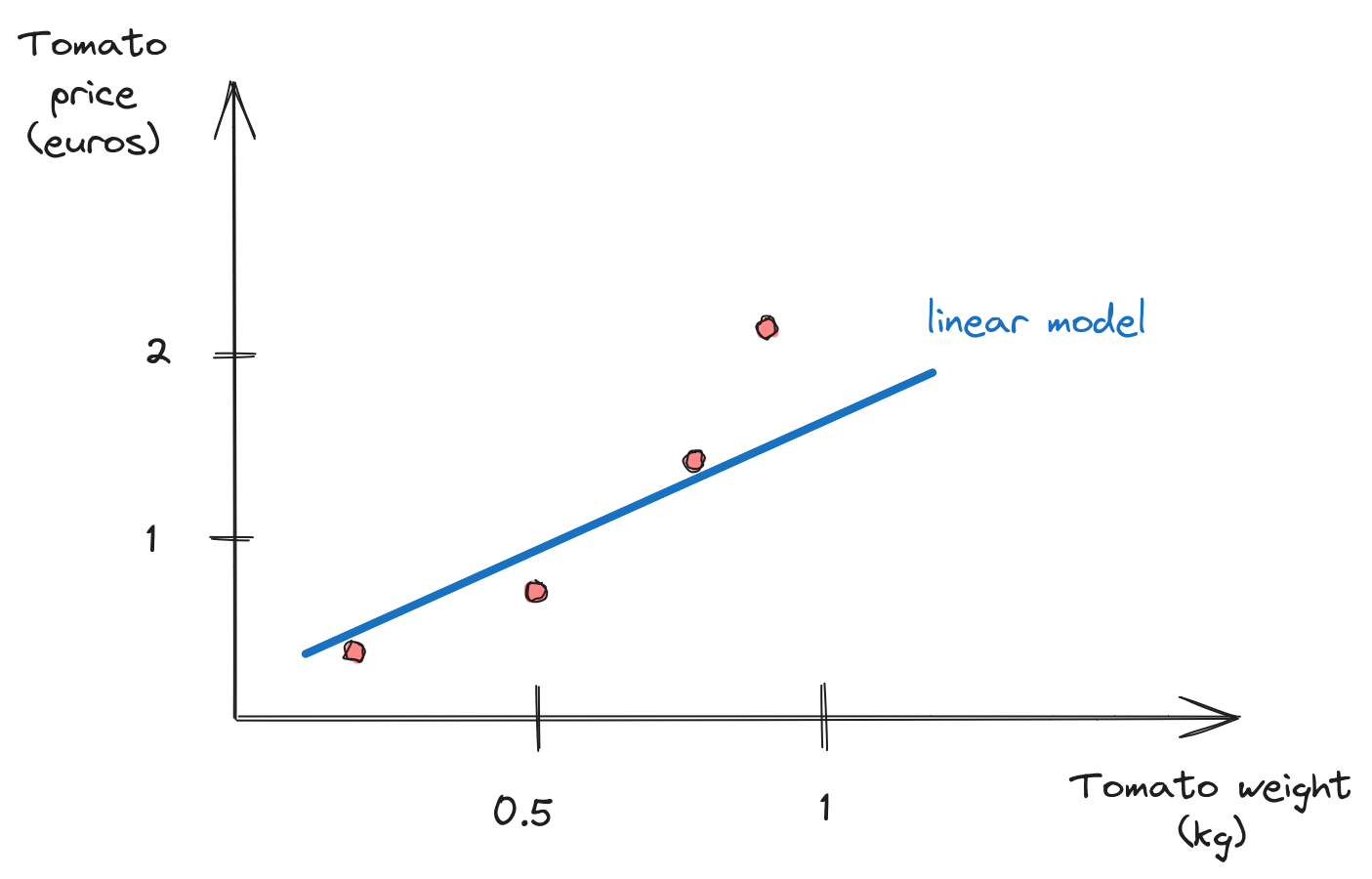
Linear model
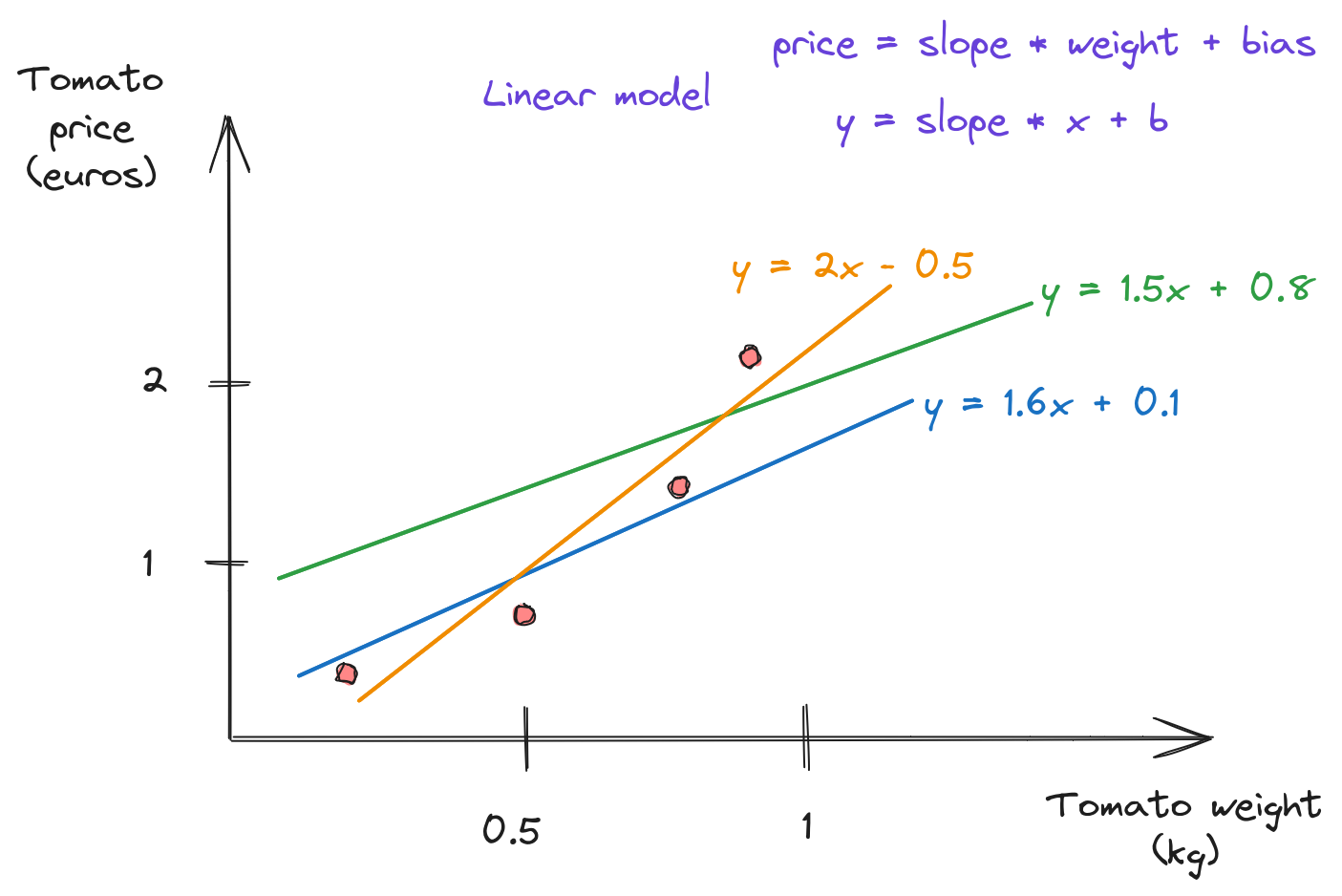
Linear model(s)?
y=fθ(x);θ={slope,bias}
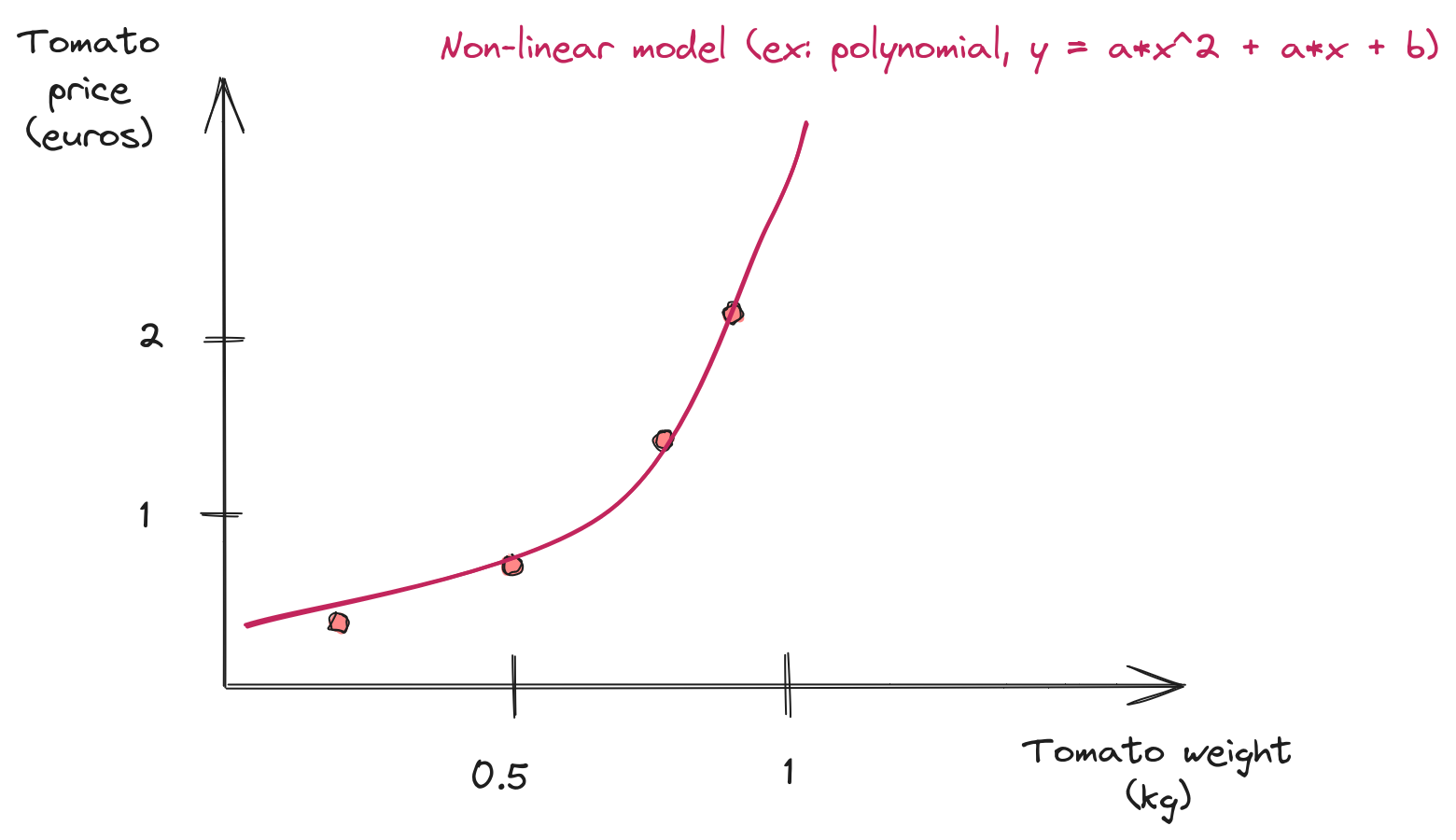
Non Linear Model
Scikit-Learn API
import numpy as np from sklearn.linear_model import LinearRegression # Generate some data (noisy linear function) x = np.linspace(0, 5, num=50).reshape(50, 1) y = 2 * x + 10 + 0.1 * np.random.rand() # Fit a linear model using least squares model = LinearRegression().fit(x, y) y_predict = model.predict(x) # Retrieve the optimized parameters slope, bias = model.coef_, model.intercept_
import numpy as np from sklearn.linear_model import LinearRegression # Generate some data (noisy linear function) x = np.linspace(0, 5, num=50).reshape(50, 1) y = 2 * x + 10 + 0.1 * np.random.rand() # Fit a linear model using least squares model = LinearRegression().fit(x, y) y_predict = model.predict(x) # Retrieve the optimized parameters slope, bias = model.coef_, model.intercept_
import numpy as np from sklearn.linear_model import LinearRegression # Generate some data (noisy linear function) x = np.linspace(0, 5, num=50).reshape(50, 1) y = 2 * x + 10 + 0.1 * np.random.rand() # Fit a linear model using least squares model = LinearRegression().fit(x, y) y_predict = model.predict(x) # Retrieve the optimized parameters slope, bias = model.coef_, model.intercept_
import numpy as np from sklearn.linear_model import LinearRegression # Generate some data (noisy linear function) x = np.linspace(0, 5, num=50).reshape(50, 1) y = 2 * x + 10 + 0.1 * np.random.rand() # Fit a linear model using least squares model = LinearRegression().fit(x, y) y_predict = model.predict(x) # Retrieve the optimized parameters slope, bias = model.coef_, model.intercept_
import numpy as np from sklearn.linear_model import LinearRegression # Generate some data (noisy linear function) x = np.linspace(0, 5, num=50).reshape(50, 1) y = 2 * x + 10 + 0.1 * np.random.rand() # Fit a linear model using least squares model = LinearRegression().fit(x, y) y_predict = model.predict(x) # Retrieve the optimized parameters slope, bias = model.coef_, model.intercept_
From Tabular Q-Learning to DQN Antonin RAFFIN ( @araffin2 ) German Aerospace Center (DLR) https://araffin.github.io/