www.dlr.de · Antonin RAFFIN · RL on real robots · RL Dresden · 15.09.2022

Training RL agents directly
on real robots

DLR bert
Antonin RAFFIN ( @araffin2 )
German Aerospace Center (DLR)
https://araffin.github.io/

Who am I?

SB

Stable-Baselines

ENSTAR

bert

HASy

David (aka HASy)

DLR

German Aerospace Center (DLR)

Outline

  1. Why learn directly on real robots?
  2. Learning from scratch
  3. Knowledge guided RL
  4. Questions?

Why learn directly on real robots?

Miki, Takahiro, et al. "Learning robust perceptive locomotion for quadrupedal robots in the wild." Science Robotics (2022)

Rudin, Nikita, et al. "Learning to walk in minutes using massively parallel deep reinforcement learning." CoRL. PMLR, 2022.

Simulation is all you need?

sim broken

Credits: Nathan Lambert (@natolambert)

Simulation is all you need? (bis)

Simulation is really all you need

Why learn directly on real robots?

  • because you can! (software/hardware)
  • simulation is safer, faster
  • simulation to reality (sim2real): accurate model and randomization needed
  • challenges: robot safety, sample efficiency

Learning from scratch

Learning to control an elastic robot

Challenges
  • hard to model (silicon neck)
  • oscillations
  • 2h on the real robot (safety)
david head

Raffin, Antonin, Jens Kober, and Freek Stulp. "Smooth exploration for robotic reinforcement learning." CoRL. PMLR, 2022.

Smooth Exploration for Robotic RL

Independent Gaussian noise: \[ \epsilon_t \sim \mathcal{N}(0, \sigma) \] \[ a_t = \mu(s_t; \theta_{\mu}) + \epsilon_t \]
State dependent exploration: \[ \theta_{\epsilon} \sim \mathcal{N}(0, \sigma_{\epsilon}) \] \[ a_t = \mu(s_t; \theta_{\mu}) + \epsilon(s_t; \theta_{\epsilon}) \]
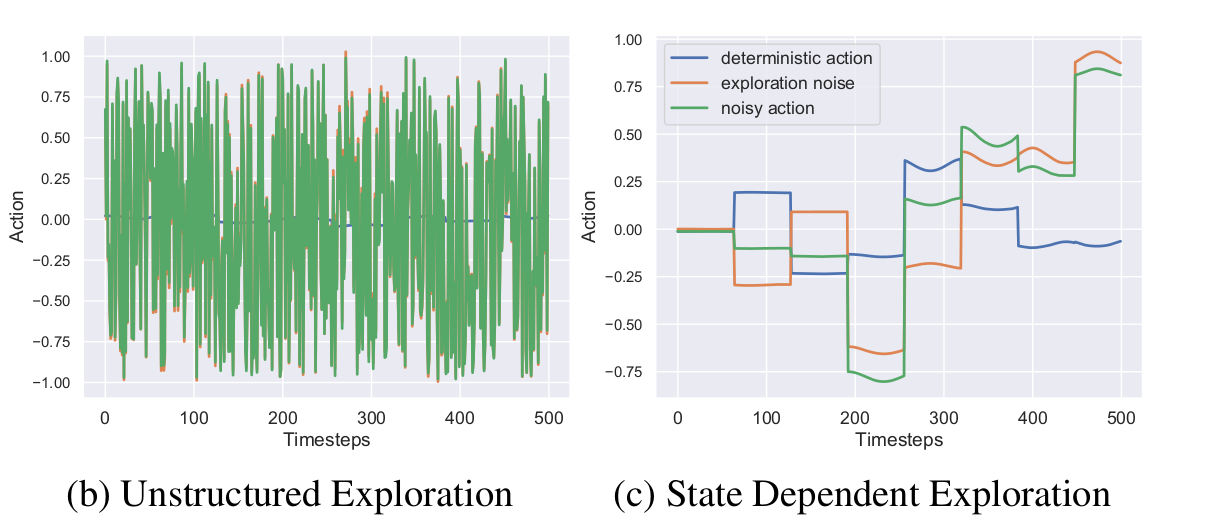
gSDE vs Independent noise

Result

Learning to walk with an elastic quadruped robot

Challenges
  • robot safety (5h+ of training)
  • manual reset
  • communication delay
bert

Raffin, Antonin, Jens Kober, and Freek Stulp. "Smooth exploration for robotic reinforcement learning." CoRL. PMLR, 2022.

DroQ - 20 Minutes Training

Smith, Laura, Ilya Kostrikov, and Sergey Levine. "A Walk in the Park: Learning to Walk in 20 Minutes With Model-Free Reinforcement Learning." arXiv preprint (2022).

Knowledge guided RL

  • knowledge about the task (frozen encoder)
  • knowledge about the robot (neck)
  • RL for improved robustness (CPG + RL)

Learning to drive in minutes / learning to race in hours

Challenges
  • minimal number of sensors (image, speed)
  • variability of the scene (light, shadows, other cars, ...)
  • limited computing power
  • communication delay
Racing car

Raffin, Antonin, Jens Kober, and Freek Stulp. "Smooth exploration for robotic reinforcement learning." CoRL. PMLR, 2022.

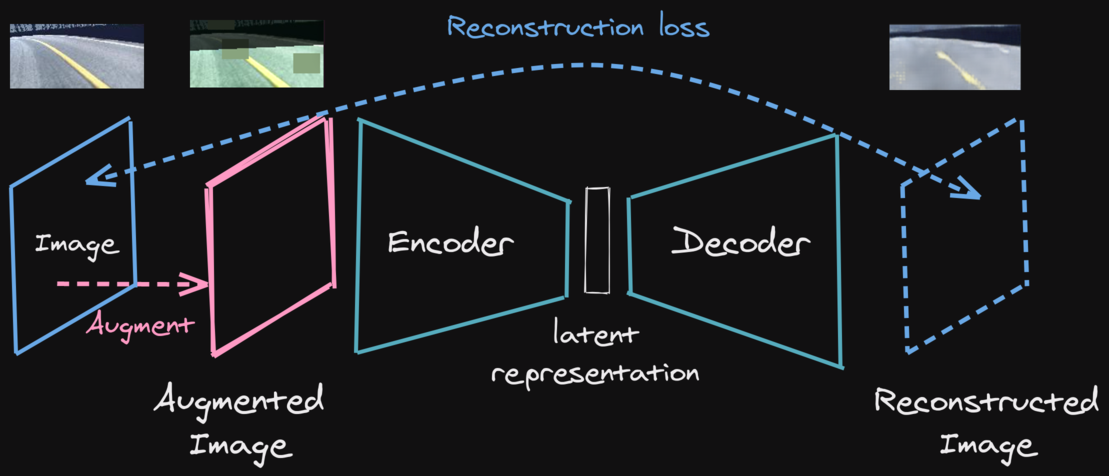
Learning a state representation (SRL)

augmented auto-encoder

References: Augmented Autoencoders (Sundermeyer et al.), Decoupling Feature Extraction from Policy Learning (Raffin et al.), SRL-Toolbox, Learning To Drive Smoothly in Minutes, Sim Siam (Chen&He)...

Pre-trained agent on Huggingface hub

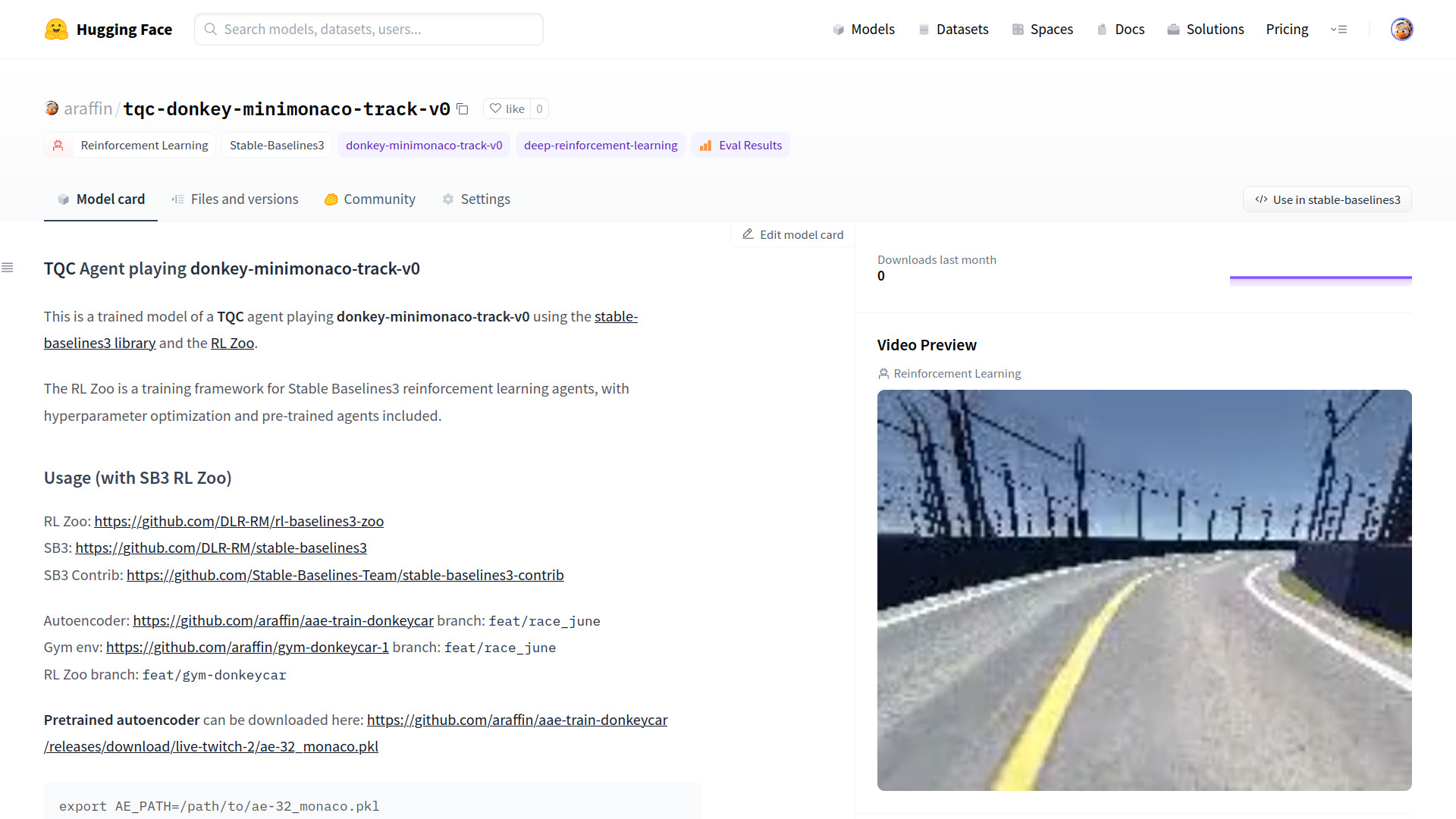
Video Serie on YouTube

Learning to Exploit Elastic Actuators for Quadruped Locomotion

Raffin et al. "Learning to Exploit Elastic Actuators for Quadruped Locomotion" In preparation ICRA, 2023.

Otimized CPG + RL

Coupled oscillator

\[\begin{aligned} \dot{r_i} & = a (\mu - r_i^2)r_i \\ \dot{\varphi_i} & = \omega + \sum_j \, r_j \, c_{ij} \, \sin(\varphi_j - \varphi_i - \Phi_{ij}) \\ \end{aligned} \]

Desired foot position

\[\begin{aligned} x_{des,i} &= \textcolor{#5f3dc4}{\Delta x_\text{len}} \cdot r_i \cos(\varphi_i)\\ z_{des,i} &= \Delta z \cdot \sin(\varphi_i) \\ \Delta z &= \begin{cases} \textcolor{#5c940d}{\Delta z_\text{clear}} &\text{if $\sin(\varphi_i) > 0$ (\textcolor{#0b7285}{swing})}\\ \textcolor{#d9480f}{\Delta z_\text{pen}} &\text{otherwise (\textcolor{#862e9c}{stance}).} \end{cases} \end{aligned} \]

closing the loop with RL

\[\begin{aligned} x_{des,i} &= \textcolor{#a61e4d}{\Delta x_\text{len} \cdot r_i \cos(\varphi_i)} + \textcolor{#1864ab}{\pi_{x,i}(s_t)} \\ z_{des,i} &= \textcolor{#a61e4d}{\Delta z \cdot \sin(\varphi_i)} + \textcolor{#1864ab}{\pi_{z,i}(s_t)} \end{aligned} \]

Fast Trot (~30 minutes training)

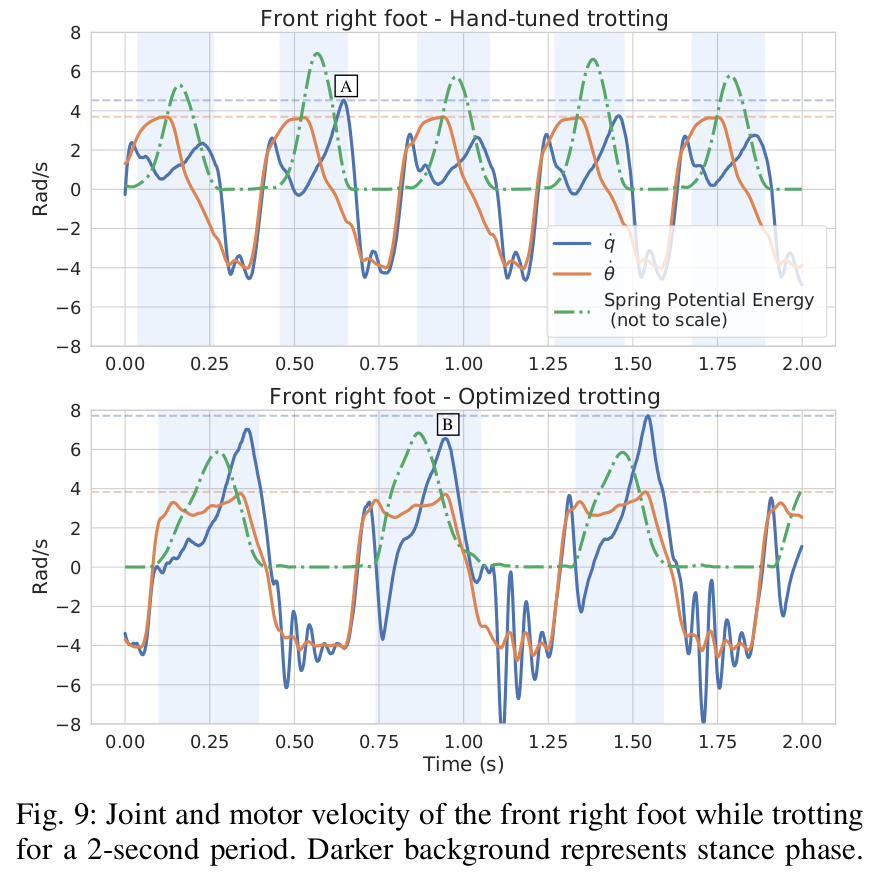
Learning to Exploit Elastic Actuators

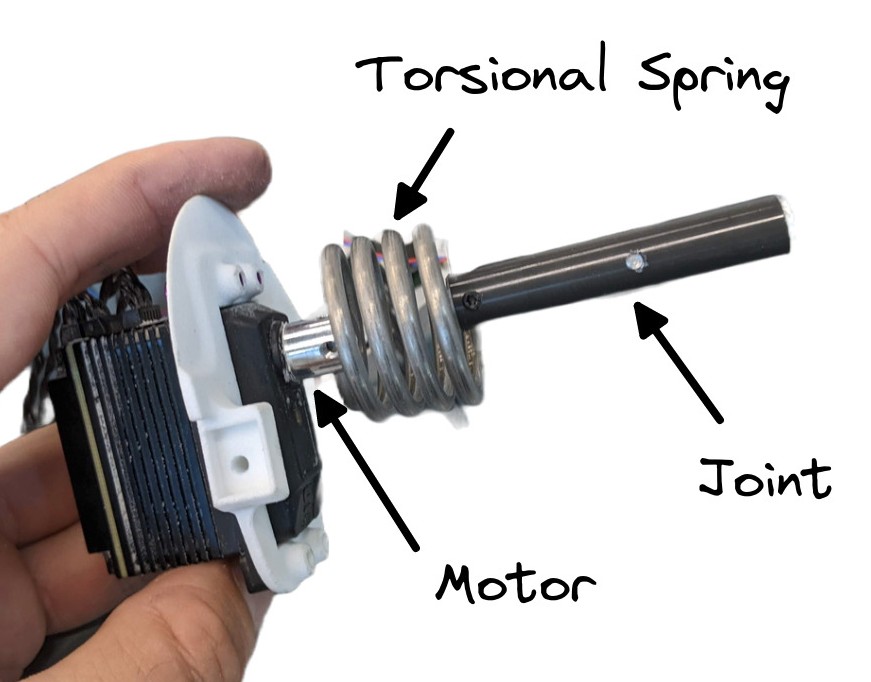
Stabilizing Pronking (1)

Stabilizing Pronking (2)

Stabilizing Pronking (3)

Patterns

Recap

  • simulation is all you need
  • learning directly on a real robot is possible
  • knowledge guided RL to improve efficiency

Questions?

Additional References

RLVS: RL in practice: tips & tricks
ICRA Tutorial: Tools for Robotic Reinforcement Learning

Backup slides

Continuity Cost

  • formulation: \[ r_{continuity} = - (a_t - a_{t - 1})^2 \]
  • requires a history wrapper

References: generalized State-Dependent Exploration (gSDE), CAPS