Recent Advances in Reinforcement Learning for Continuous Control

www.dlr.de · Antonin RAFFIN · Recent Advances in RL for Continuous Control · CERN ML Workshop · 21.05.2025

Recent Advances in RL for Continuous Control

Antonin RAFFIN (@araffin.bsky.social)
German Aerospace Center (DLR)
https://araffin.github.io/

RL 101

Two lines of improvements

Sample efficiency
Ex: real robot, slow simulation

Speed
Ex: fast simulation on GPU, slow algorithm

Outline

RL 102 (from DQN to SAC)
Advances in Algorithms
Advances in Software
Advances in Simulators

From DQN to SAC (in 10 minutes)

Deep Q-Network (DQN)

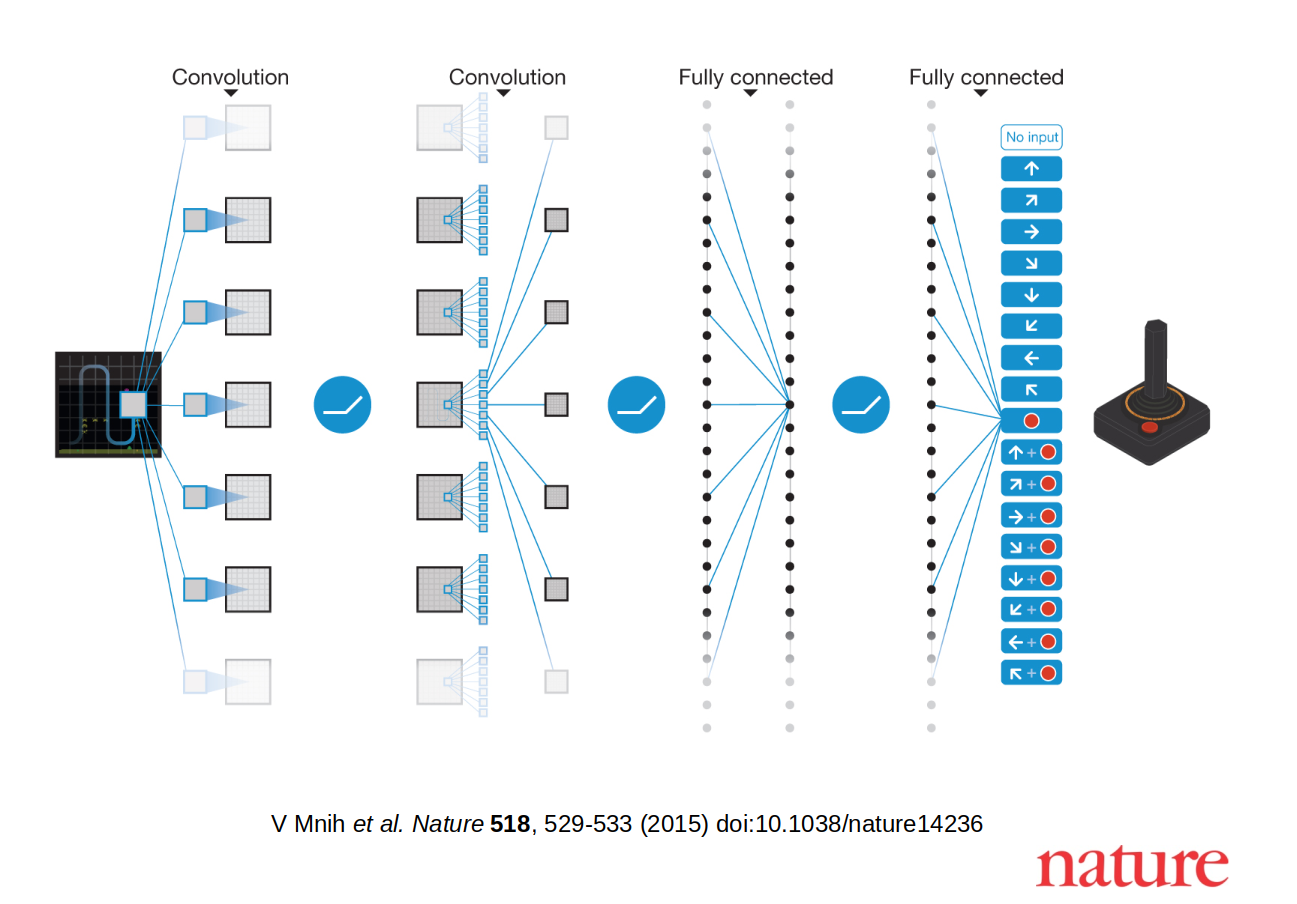
Mnih, Volodymyr, et al. "Playing atari with deep reinforcement learning." (2013).

RL Objective

Maximize the sum of discounted reward

\[\begin{aligned} J(\pi) = \mathop{\mathbb{E}}[r_0 + \gamma r_{1} + \gamma^2 r_{2} + ...]. \end{aligned} \]

Action-Value Function: $Q$-Value

How good is it to take action $a$ in state $s$?

\[\begin{aligned} Q^\pi(s, a) = \mathop{\mathbb{E}}[r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + ... | s_t=s, a_t=a]. \end{aligned} \]

\[\begin{aligned} \pi(s) = \argmax_{a \in A} Q^\pi(s, a) \end{aligned} \]

Bellman equation (practical): \[\begin{aligned} Q^{\pi}(s, a) &= \mathbb{E}[r_t + \gamma \mathbb{E}_{a'\sim \pi}{Q^{\pi}(s_{t+1},a')}]. \end{aligned}\]

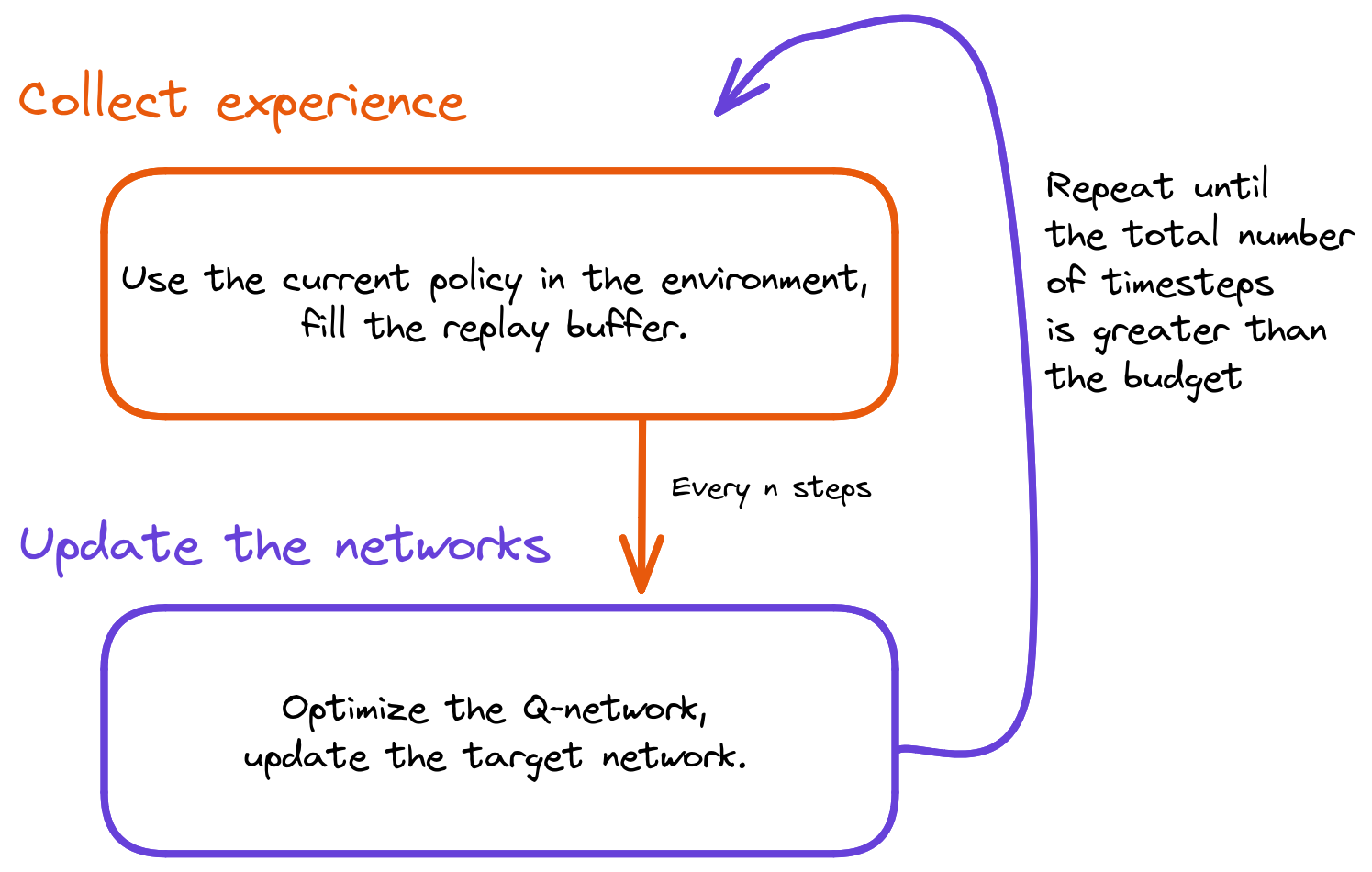
DQN Components

RL Summer School 2023 - DQN Tutorial

The training loop

Extending DQN to Continuous Actions (DDPG)

Discrete actions: \[\begin{aligned} \pi(s) = \argmax_{a \in A} Q^\pi(s, a) \end{aligned} \]

Learn to maximize the $Q$-function using $\pi_{\phi}$.

\[\begin{aligned} \max_{a \in A} Q_\theta(s, a) \approx Q_\theta(s, \pi_{\phi}(s)). \end{aligned} \]

Lillicrap, Timothy P., et al. "Continuous control with deep reinforcement learning." (2015).

Deep Deterministic Policy Gradient (DDPG)

Overestimation bias

TD3: select the min of $Q^1_\theta$ and $Q^2_\theta$

Fujimoto, Scott, Herke Hoof, and David Meger. "Addressing function approximation error in actor-critic methods." (2018).

Soft Actor-Critic (SAC)

SAC $\approx$ DQN + DDPG + TD3 + Maximum entropy RL

Maximum entropy RL: encourage exploration while still solving the task

\[\begin{aligned} J(\pi) = \mathop{\mathbb{E}}[\sum_{t}{\textcolor{darkblue}{\gamma^t r(s_t, a_t)} + \textcolor{darkgreen}{\alpha\mathcal{H}(\pi({\,\cdot\,}|s_t))}}]. \end{aligned} \]

Ex: Avoid the variance of the Gaussian distribution to collapse too early

Haarnoja, Tuomas, et al. "Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor." (2018).

Questions?

Annotated DQN Algorithm

Outline

RL 102 (from DQN to SAC)
Advances in Algorithms
Advances in Software
Advances in Simulators

Beyond SAC: TQC, DroQ, SimBa, ...

Stochastic Environments

Same state $s_t$, same action $a_t$, different outcome $r(s_t, a_t)$

Distributional RL

TQC $\approx$ SAC + quantile regression (truncated)

Kuznetsov, Arsenii, et al. "Controlling overestimation bias with truncated mixture of continuous distributional quantile critics." (2020).

TQC Results

Higher replay ratio (REDQ, DroQ)

Idea: re-use samples from the replay buffer more

Issue: Naive scaling doesn't work (overestimation, extrapolation errors, ...)

Solution? explicit (REDQ)/ implicit (DroQ) ensembles, regularization, ...

Chen, Xinyue, et al. "Randomized ensembled double q-learning: Learning fast without a model." (2021).
Hiraoka, Takuya, et al. "Dropout q-functions for doubly efficient reinforcement learning." (2021).
D'Oro, Pierluca, et al. "Sample-efficient reinforcement learning by breaking the replay ratio barrier." (2022).
Hussing, Marcel, et al. "Dissecting deep rl with high update ratios: Combatting value overestimation and divergence." (2024).