Who am I?

Stable-Baselines

bert

David (aka HASy)

German Aerospace Center (DLR)
RL is Hard
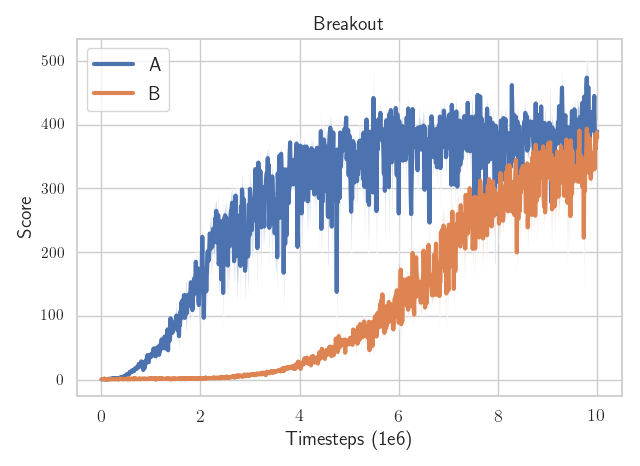
Which algorithm is better?
The only difference: the epsilon $\epsilon$ value to avoid division by zero in the optimizer
(one is $\epsilon$ = 1e-7
the other $\epsilon$ = 1e-5)
Reproducibility Findings
Agarwal, Rishabh, et al. "Deep reinforcement learning at the edge of the statistical precipice." Neurips (2021)
Outline
- SB3: Reliable RL Implementations
- RL Zoo: Reproducible Experiments
- Implementing a New Algorithm
- Minimal Implementations
- Best Practices for Empirical RL
- Questions?
Stable-Baselines3


Reliable Implementations?

- Performance checked
- Software best practices (96% code coverage, type checked, ...)
- 3 types of tests (run, unit tests, performance)
- Active community (6000+ stars, 1000+ citations, 3M+ downloads)
- Fully documented
Performance Test Example
# Training budget (cap the max number of iterations)
N_STEPS = 1000
def test_ppo():
agent = PPO("MlpPolicy", "CartPole-v1").learn(N_STEPS)
# Evaluate the trained agent
episodic_return = evaluate_policy(agent, n_eval_episodes=20)
# check that the performance is above a given threshold
assert episodic_return > 90
SB3 Ecosystem
Smooth Exploration for RL
Raffin, Antonin, Jens Kober, and Freek Stulp. "Smooth exploration for robotic reinforcement learning." CoRL. PMLR, 2022.
SB3 + RL Zoo

RL Zoo: Reproducible Experiments
- Training, loading, plotting, hyperparameter optimization
- W&B and Huggingface integration
- 200+ trained models with tuned hyperparameters
- OpenRL Benchmark

In practice
# Train an SAC agent on Pendulum using tuned hyperparameters,
# evaluate the agent every 1k steps and save a checkpoint every 10k steps
# Pass custom hyperparams to the algo/env
python -m rl_zoo3.train --algo sac --env Pendulum-v1 --eval-freq 1000 \
--save-freq 10000 -params train_freq:2 --env-kwargs g:9.8
sac/
└── Pendulum-v1_1 # One folder per experiment
├── 0.monitor.csv # episodic return
├── best_model.zip # best model according to evaluation
├── evaluations.npz # evaluation results
├── Pendulum-v1
│ ├── args.yml # custom cli arguments
│ ├── config.yml # hyperparameters
│ └── vecnormalize.pkl # normalization
├── Pendulum-v1.zip # final model
└── rl_model_10000_steps.zip # checkpoint
Plotting
python -m rl_zoo3.cli all_plots -a sac -e HalfCheetah Ant -f logs/ -o sac_results
python -m rl_zoo3.cli plot_from_file -i sac_results.pkl -latex -l SAC --rliable

Open RL Benchmark
Learning to Exploit Elastic Actuators
Raffin et al. "Learning to Exploit Elastic Actuators for Quadruped Locomotion" In preparation, 2023.
Learning to race in an hour
Implementing a New Algorithm


1. Read the original paper several times


2. Read existing implementations (if available)

The 37 Implementation Details of Proximal Policy Optimization
3. Try to have some "sign of life" on toy problems
Iterate quickly!


4. Step by step validation
Log useful values, ipdb, visualize

5. Validation on known environments
Easy ➤ Medium ➤ Hard



Some Examples
- SB2 PPO: broadcast error
- SB3 A2C: TF RMSProp ≠ PyTorch RMSProp
- SBX DQN: target network not updated
More in the backup slides | 7 mistakes challenge
RL from scratch in 10 minutes
Using SB3 + Jax = SBX: https://github.com/araffin/sbx
From complex codebase to minimal implementation

Minimal Implementations
- Standalone / minimal dependencies
- Reduce complexity
- Easier to share/reproduce
- Perfect for educational purposes (cleanRL)
- Find bugs
- Hard to maintain

Example
A Simple Open-Loop Baseline for RL Locomotion Tasks

Raffin et al. "A Simple Open-Loop Baseline for RL Locomotion Tasks" In preparation, ICLR 2024.
35 lines of code
Sim2real transfer
Best Practices for Empirical RL
Conclusion
- Tips for reliable implementations
- Reproducible experiments
- Implementing a new algorithm
- Minimal implementations to the rescue
- Follow best practices
Questions?
Backup Slides
Huggingface Integration
Benchmarking New Implementations
- Read the original paper several times
- Read existing implementations (if available)
- Try to have some "sign of life" on toy problems
- Step by step validation (
ipdb, log useful values, visualize) - Validation on known envs (might require tuning)

The 37 Implementation Details of Proximal Policy Optimization
Nuts and Bolts of Deep RL Experimentation
Some bugs
Proper Handling of Timeouts
# Note: done = terminated or truncated
# Offpolicy algorithms
# If the episode is terminated, set the target to the reward
should_bootstrap = np.logical_not(replay_data.terminateds)
# 1-step TD target
td_target = replay_data.rewards + should_bootstrap * (gamma * next_q_values)
# On-policy algorithms
if truncated:
terminal_reward += gamma * next_value
35 lines of code
import gymnasium as gym
import numpy as np
from gymnasium.envs.mujoco.mujoco_env import MujocoEnv
# Env initialization
env = gym.make("Swimmer-v4", render_mode="human")
# Wrap to have reward statistics
env = gym.wrappers.RecordEpisodeStatistics(env)
mujoco_env = env.unwrapped
n_joints = 2
assert isinstance(mujoco_env, MujocoEnv)
# PD Controller gains
kp, kd = 10, 0.5
# Reset the environment
t, _ = 0.0, env.reset(seed=0)
# Oscillators parameters
omega = 2 * np.pi * 0.62 * np.ones(n_joints)
phase = 2 * np.pi * np.array([0.00, 0.95])
while True:
env.render()
# Open-Loop Control using oscillators
desired_qpos = np.sin(omega * t + phase)
# PD Control: convert to torque, desired qvel is zero
desired_torques = (
kp * (desired_qpos - mujoco_env.data.qpos[-n_joints:])
- kd * mujoco_env.data.qvel[-n_joints:]
)
desired_torques = np.clip(desired_torques, -1.0, 1.0) # clip to action bounds
_, reward, terminated, truncated, info = env.step(desired_torques)
t += mujoco_env.dt
if terminated or truncated:
print(f"Episode return: {float(info['episode']['r']):.2f}")
t, _ = 0.0, env.reset()




