Automatic Hyperparameter Tuning - In Practice (Part 2)

This is the second (and last) post on automatic hyperparameter optimization. In the first part, I introduced the challenges and main components of hyperparameter tuning (samplers, pruners, objective function, …). This second part is about the practical application of this technique with the Optuna library, in a reinforcement learning setting (using the Stable-Baselines3 (SB3) library).

Code: https://gist.github.com/araffin/d16e77aa88ffc246856f4452ab8a2524

Note: if you prefer to learn with video, I gave this tutorial at ICRA 2022. The slides, notebooks and videos are online:

PPO on Pendulum-v1 - When default hyperparameters don’t work

To make this post more concrete, let’s take a simple example where the default hyperparameters don’t work. In the Pendulum-v1 environment, the RL agent controls a pendulum that “starts in a random position, and the goal is to swing it up so it stays upright”.

Trained SAC agent on the Pendulum-v1 environment.

The agent receives the state of the pendulum as input (cos and sine of the angle $\theta$ and angular velocity $\dot{\theta}$) and outputs the desired torque (1D). The agent is rewarded for keeping the pendulum upright ($\theta = 0$ and $\dot{\theta} = 0$) and penalized for using high torques. An episode ends after a timeout of 200 steps ( truncation).

If you try to run the Proximal Policy Optimization (PPO) algorithm on the Pendulum-v1 environment, with a budget of 100,000 timesteps (SAC can solve this task in only 5,000 steps), it will not converge¹. With the default hyperparameters, you will get an average return of about -1000, far from the best performance you can get, which is around -200:

from stable_baselines3 import PPO
# Faster, with Jax: from sbx import PPO

# Default hyperparameters don't work well
PPO("MlpPolicy", "Pendulum-v1", verbose=1).learn(100_000, progress_bar=True)

Defining the Search Space

The first thing to define when optimizing hyperparameters is the search space: what parameters to optimize and what range to explore? You need also to decide from which distribution to sample from. For example, in the case of continuous variables (like the discount factor $\gamma$ or the learning rate $\alpha$), values can be sampled from a uniform or log-uniform distribution.

Sampling methods

In practice, Optuna provides several trial.suggest_... methods to define which parameter to optimize with which distribution. For instance, to sample the discount factor $\gamma$ uniformly from the range $[0, 1]$, you would use gamma = trial.suggest_float("gamma", 0.0, 1.0).

I recommend reading the Optuna documentation to have a better understanding of the library and its features. In the meantime, you need to know about some other useful methods for sampling hyperparameters:

• trial.suggest_float(..., log=True) to sample from a log-uniform distribution (ex: learning rate)
• trial.suggest_int("name", low, high) to sample integers (ex: mini-batch size), low and high are included
• trial.suggest_categorical("name", choices) for sampling from a list of choices (ex: choosing an activation function)

Back to the PPO example on the Pendulum-v1 task, what hyperparameters can be optimized and what range should be explored for each of them?

PPO hyperparameters

PPO has many hyperparameters, but to keep the search small (and this blog post short), I will limit the search to four parameters: the learning rate $\alpha$, the discount factor $\gamma$, the activation function of the neural networks and the number of steps for data collection (n_steps).

Tuning the learning rate $\alpha$ is crucial for fast but stable training. If $\alpha$ is too big, the training tends to be unstable and usually leads to NaNs (or other numerical instability). If it is too small, it will take forever to converge.

Since the learning rate $\alpha$ is a continuous variable (it is a float) and distinguishing between small learning rates is important, it is recommended to use a log-uniform distribution for sampling. To search around the default learning rate $\alpha_0 = 3e^{-4}$, I define the search space to be in $[\alpha_0 / 10, 10 \alpha_0] = [3e^{-5}, 3e^{-3}]$. This translates to learning_rate = trial.suggest_float("learning_rate", 3e-5, 3e-3, log=True) with Optuna.

The discount factor $\gamma$ represents a trade-off between optimizing short-term rewards and long-term rewards. In general, we want to maximize the sum of undiscounted rewards ($\gamma = 1$), but in practice $\gamma < 1$ works best (while keeping $\gamma \approx 1$). A recommended range for the discount factor $\gamma$ is $[0.97, 0.9999]$² (default is 0.99), or in Python: gamma = trial.suggest_float("gamma", 0.97, 0.9999).

I’m considering two activation functions in this example: Tanh and ReLU. Because the activation function is sampled from a list of options, activation_fn = trial.suggest_categorical("activation_fn", ["tanh", "relu"]) is the corresponding code³.

Finally, PPO has a n_steps parameter that controls the “number of steps to run for each environment per update”. That is to say, PPO updates its policy every n_steps * n_envs steps (and collect n_steps * n_envs transitions to sample from). This hyperparameter also affects the value and advantage estimation (larger n_steps leads to less biased estimates). It is recommended to use a power of two for its value⁴, i.e., we sample the exponent instead of the value directly, which translates to n_steps_pow = trial.suggest_int("n_steps_pow", 5, 12) (from $2^5=32$ to $2^{12}=4096$).

To summarize, this is the overall sampling function:

from typing import Any

import optuna

def sample_ppo_params(trial: optuna.Trial) -> dict[str, Any]:
    """Sampler for PPO hyperparameters."""
    # From 2**5=32 to 2**12=4096
    n_steps_pow = trial.suggest_int("n_steps_pow", 5, 12)
    gamma = trial.suggest_float("one_minus_gamma", 0.97, 0.9999)
    learning_rate = trial.suggest_float("learning_rate", 3e-5, 3e-3, log=True)
    activation_fn = trial.suggest_categorical("activation_fn", ["tanh", "relu"])
    # Convert power of two to number of steps
    n_steps = 2**n_steps_pow
    # Display true values
    trial.set_user_attr("n_steps", n_steps)
    # Convert to PyTorch objects
    activation_fn = {"tanh": nn.Tanh, "relu": nn.ReLU}[activation_fn]

    return {
        "n_steps": n_steps,
        "gamma": gamma,
        "learning_rate": learning_rate,
        "policy_kwargs": {
            "activation_fn": activation_fn,
        },
    }

Defining the Objective Function

After choosing the search space, you need to define the objective function. In reinforcement learning, we usually want to get the best performance for a given budget (either in terms of samples or training time), i.e., we try to maximize the episodic reward.

One way to measure the performance is to periodically evaluate the agent on a test environment for multiple episodes:

from stable_baselines3.common.evaluation import evaluate_policy
# model = PPO("MlpPolicy", "Pendulum-v1")
# eval_env = gym.make("Pendulum-v1")
# Note: by default, evaluate_policy uses the deterministic policy
mean_return, std_return = evaluate_policy(model, eval_env, n_eval_episodes=20)

In practice, with SB3, I use a custom callback to trigger evaluations at different stages of training:

from stable_baselines3.common.callbacks import BaseCallback

class TrialEvalCallback(BaseCallback):
    """Callback used for evaluating and reporting a trial."""

    def _on_step(self) -> bool:
        if self.eval_freq > 0 and self.n_calls % self.eval_freq == 0:
            # Evaluate the current policy every n_calls
            mean_return, _ = evaluate_policy(self.model, self.eval_env)
            self.eval_idx += 1
            # Send report to Optuna
            self.trial.report(mean_return, self.eval_idx)
            # Prune (stop training) trial if needed
            if self.trial.should_prune():
                self.is_pruned = True
                return False
        return True

This callback also allows to stop training early if a trial is too bad and should be pruned (by checking the value of trial.should_prune()).

The full objective method contains additional code to create the training environment, sample the hyperparameters, instantiate the RL agent and train it:

from stable_baselines3.common.env_util import make_vec_env

N_ENVS = 5
N_TIMESTEPS = 40_000
# Evaluate every 20_000 steps
# each vec_env.step() is N_ENVS steps
EVAl_FREQ = 20_000 // N_ENVS

def objective(trial: optuna.Trial) -> float:
    # Create train and eval envs,
    # I use multiple envs in parallel for faster training
    vec_env = make_vec_env("Pendulum-v1", n_envs=N_ENVS)
    eval_env = make_vec_env("Pendulum-v1", n_envs=N_ENVS)
    # Sample hyperparameters. and create the RL model
    model = PPO("MlpPolicy", vec_env, **sample_ppo_params(trial))

    # Create the callback that will periodically evaluate and report the performance.
    eval_callback = TrialEvalCallback(
        eval_env,
        trial,
        n_eval_episodes=20,
        eval_freq=EVAl_FREQ, 
    )
    # Train the RL agent
    model.learn(N_TIMESTEPS, callback=eval_callback)

    if eval_callback.is_pruned:
        raise optuna.exceptions.TrialPruned()
    # Report final performance
    return eval_callback.last_mean_reward

Choosing Sampler and Pruner

Finally, after defining the search space and the objective function, you have to choose a sampler and (optionally) a pruner (see part one). If you don’t know what to choose, Optuna now has an AutoSampler which choosees a recommended sampler for you (between TPESampler, GPSampler and CmaEsSampler), based on heuristics.

Here, I selected TPESampler and MedianPruner because they tend to be good default choices. Don’t forget to pass n_startup_trials to both to warm up the optimization with a RandomSampler (uniform sampler) and to avoid premature convergence (like pruning potentially good trials too early):

from optuna.pruners import MedianPruner
from optuna.samplers import TPESampler, RandomSampler
 
# Select the sampler, can be random, TPESampler, CMAES, ...
sampler = TPESampler(n_startup_trials=5)
# Do not prune before 1/3 of the max budget is used
pruner = MedianPruner(n_startup_trials=5, n_warmup_steps=N_EVALUATIONS // 3)
	
# Create the study and start the hyperparameter optimization
study = optuna.create_study(sampler=sampler, pruner=pruner, direction="maximize")
# This script can be launch in parallel when using a database
# We pass the objective function defined previously
study.optimize(objective, n_trials=N_TRIALS, timeout=TIMEOUT)
# Best result
best_trial = study.best_trial

Et voilà! That’s all you need to run automatic hyperparameter optimization. If you now run the final script for five minutes, it should quickly find hyperparameters that give good results.

For example, in one of the runs I did, I was able to get in just two minutes:

Number of finished trials: 21
Best trial:
  Value:  -198.01224440000001
  Params: 
    n_steps_pow: 8
    gamma: 0.9707141699579157
    learning_rate: 0.0014974865679170315
    activation_fn: relu
  User attrs:
    n_steps: 256

To verify that these hyperparameters actually work (more on that soon), you can use:

from stable_baselines3 import PPO
from stable_baselines3.common.env_util import make_vec_env
import torch as th

vec_env = make_vec_env("Pendulum-v1", n_envs=5)
# Using optimized hyperparameters
policy_kwargs = dict(activation_fn=th.nn.ReLU)
hyperparams = dict(n_steps=256, gamma=0.97, learning_rate=1.5e-3)

model = PPO("MlpPolicy", vec_env, verbose=1, **hyperparams)
model.learn(40_000, progress_bar=False)

It should give you better results than the default hyperparameters with half of the training budget.

Note: I recommend using the RL Zoo for more complex settings. It includes automatic hyperparameter tuning, loading trial and distributed optimization. Example command to optimize PPO on the Pendulum-v1 environment:

python -m rl_zoo3.train --algo ppo --env Pendulum-v1 -optimize --storage ./demo.log --study-name demo

Distributed Optimization

A simple way to speed up the optimization process is to run multiple trials in parallel. To do this, you need to use a database and pass it to Optuna’s create_study() method.

The easiest way to distribute tuning is to use a log file for storage and start the same script in multiple terminals (and potentially on multiple machines):

storage_file = "./my_studies.log"
study_name = "ppo-Pendulum-v1_1"

storage = optuna.storages.JournalStorage(
    optuna.storages.journal.JournalFileBackend(storage_file),
)
study = optuna.create_study(
    ...
    storage=storage,
    study_name=study_name,
    load_if_exists=True,
)

If you use a database (you should), you can also use Optuna dashboard to monitor the optimization progress.

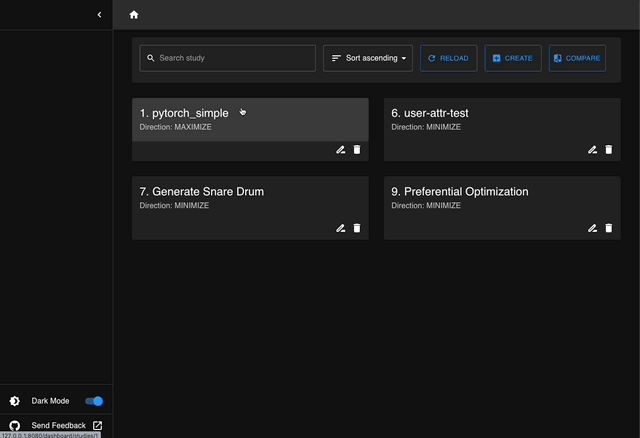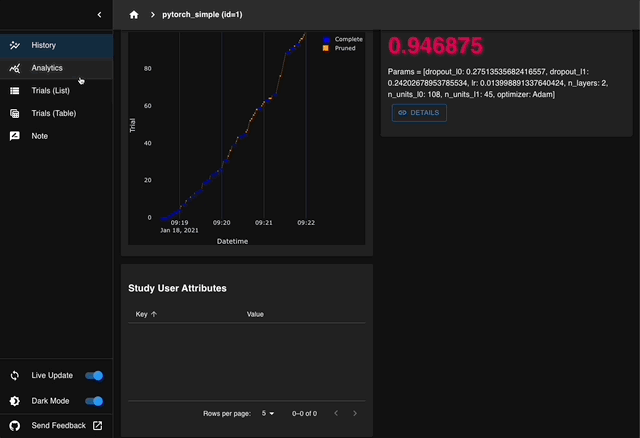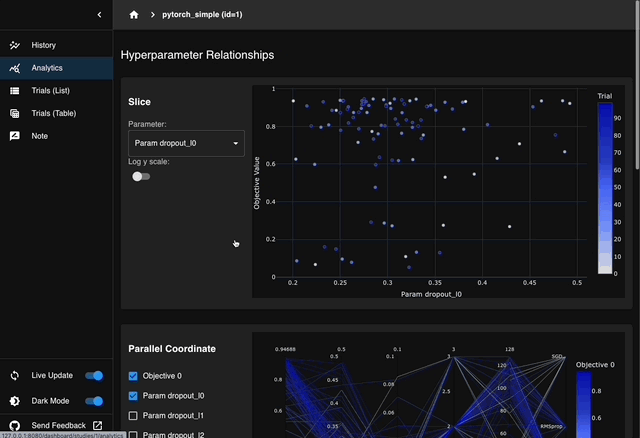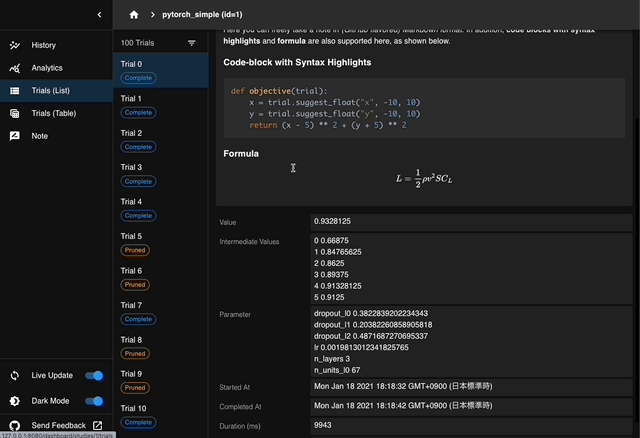
Optuna dashboard demo

Tips and Tricks

Before concluding this blog post, I would like to give you some tips and tricks to keep in mind when doing hyperparameter tuning.

Start simple

First, as with any RL problem, starting simple is the key to success. Do not try to optimize too many hyperparameters at once, using large ranges. My advice would be to start with a minimal number of parameters (i.e., start with a small search space) and increase their number and ranges only as needed.

For example, to decide whether to increase or decrease the search range, you can look at the best trials so far. If the best trials are close to the limits of the search space (saturation), this is a sign that you should increase the limits. On the other hand, if above a certain threshold for a parameter, all trials are bad, you can probably reduce the search space.

Another thing to keep in mind is that most of the time, you don’t need automatic tuning. Simply training for a longer time (i.e., using a larger training budget) can improve the results without changing the hyperparameters.

Post-Evaluation to Remove Noise

Last but not least (and perhaps the most important tip), do not forget that RL training is a stochastic process. This means that the performance reported for each trial can be noisy: if you run the same trial but with a different random seed, you might get different results.

I tend to approach this problem in two ways.

To filter out the evaluation noise, I usually re-evaluate the top trials multiple times to find out which ones were “lucky seeds” and which ones work consistently. Another way to deal with this problem is to do multiple runs per trial: each run uses the same hyperparameters but starts with a different random seed. However, this technique is expensive in terms of computation time and makes it difficult to prune out bad trials early.

Conclusion

In this second part, I went through the process of doing automatic hyperparameter tuning in practice, using the Optuna library. I’ve covered:

• defining the search space and the objective function
• choosing a sampler and a pruner
• speeding up the tuning process with distributed optimization
• tips and tricks to keep in mind when doing automatic hyperparameter tuning

As a conclusion and transition to the next blog post (WIP), I will use this technique to tune SAC for fast training when using a massively parallel environment like Isaac Sim.

PS: In case you missed it, you can find the final script here: https://gist.github.com/araffin/d16e77aa88ffc246856f4452ab8a2524

Appendix - The Optuna Library

Among the various open-source libraries for hyperparameter optimization (such as hyperopt or Ax), I chose Optuna for multitple reasons:

• it has a clean API and good documentation
• it supports many samplers and pruners
• it has some nice additional features (like easy distributed optimization support, multi-objective support or the optuna-dashboard)

Citation

@article{raffin2025optuna,
  title   = "Automatic Hyperparameter Tuning - In Practice",
  author  = "Raffin, Antonin",
  journal = "araffin.github.io",
  year    = "2025",
  month   = "April",
  url     = "https://araffin.github.io/post/optuna/"
}

Did you find this post helpful? Consider sharing it 🙌

Footnotes